強化学習入門 Part3 － AlphaGoZeroでも重要な技術要素！モンテカルロ木探索の入門－

本記事は、当社オウンドメディア「Doors」に移転しました。

約5秒後に自動的にリダイレクトします。

強化学習入門の第3弾。「モンテカルロ木探索（Monte Carlo Tree Search, MCTS）」を解説するとともに、実際にAI同士で五目並べを戦わせてみました！

こんにちは。アナリティクスサービス本部 AI開発部の山崎です。

昨年も強化学習界隈は盛り上がりを見せていましたが、今なお、強化学習と言えば一番にAlphaGoを思い浮かべる人も多いのではないでしょうか。昨年、AlphaGoZeroという進化バージョンが発表され、一切のお手本を用いずに従来バージョンより強いということが話題になりました。（それまでのAlphaGoは、人のお手本をある程度学び、その後勝手に学んでいくものでした）
さらに、AlphaGoZeroを一般化したアルゴリズムに修正したAlphaZeroが登場し、チェスや将棋でもその時点での最強ソフトを打ち負かしています。

今回は、AlphaGoやAlphaGoZero、AlphaZeroの中で使われている、強化学習と関連の深い手法の一つである「モンテカルロ木探索（Monte Carlo Tree Search, MCTS）」について説明します。
そしてブログの最後では、Tensorflow, Keras, OpenAI Gymを使って、実際に五目並べをAI同士で戦わせてみます！

0. はじめに
1. ゲーム木
2. モンテカルロ法
3. モンテカルロ木探索
- Selection
- Expansion
- Evaluation
- Backup
- Play
4. モンテカルロ木探索（AlphaZeroバージョン）
5. おわりに
■参考資料

0. はじめに

強化学習ってそもそも何だ？という人は過去記事を参照ください。
blog.brainpad.co.jp
blog.brainpad.co.jp

Part1、Part2で、stateから最適なactionを求めるいくつかのアルゴリズムを紹介しました。
ところで、囲碁のようなゲームでは、次にどんな手を打つのかについて、みんなきっとこんな風に考えながら決めているのではないでしょうか。

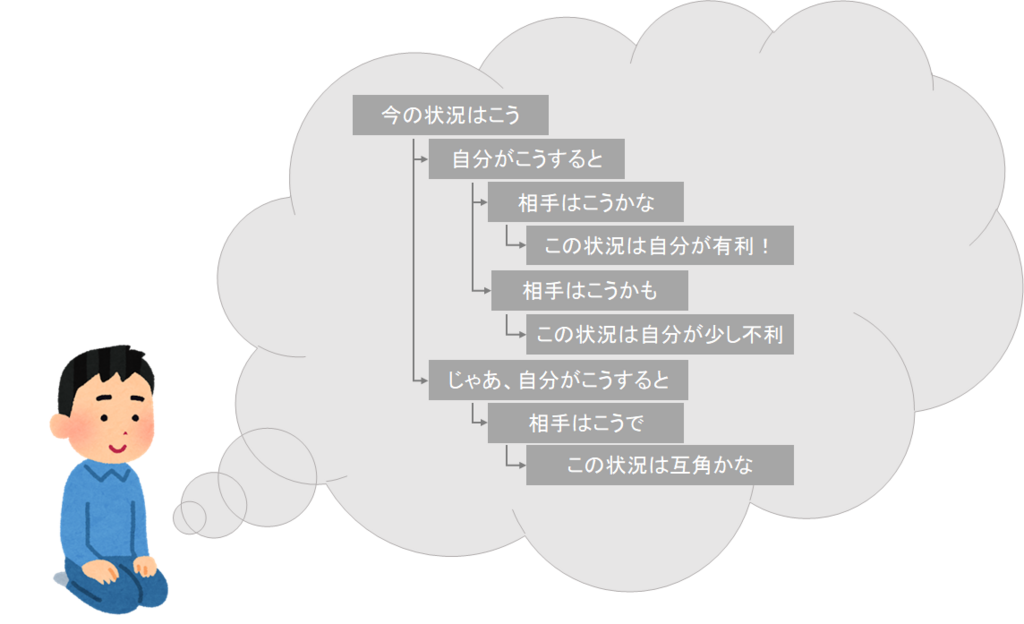
私は囲碁は打てないのですが、将棋やリバーシでは私は上記のように次の手を決めています。
いわゆる、展開を3手先まで読むとか、15手先まで読むとか言うやつですね。

実は、AlphaGoやAlphaGoZero、AlphaZeroでも、先を読んで次の手を決めているのです。

1. ゲーム木

囲碁や将棋やリバーシのようなゲームは、交互に手を選択し、選択した手によって状況が変化していきます。このようなゲームでは、ゲーム木という表現ができます。
簡単に、3目並べというゲームを用いて考えます。
（Tic Tak Toe とか、マルバツゲームとか呼ばれるゲームです。先手は●を、後手は×を、交互に盤面の空いているマスに置いていき、縦、横、斜めのいずれかに３つ、自分のマークを並べた方の勝ちです。）

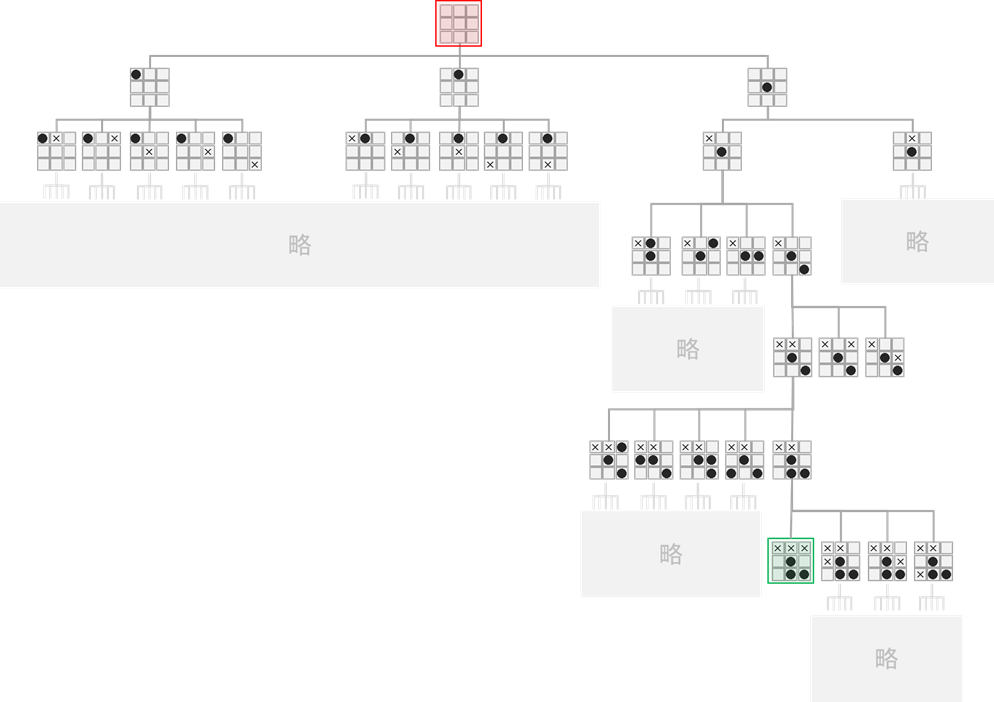
上の図は3目並べのゲーム木です。反転や回転して同じになる局面は省略しています。とても全ての展開は書ききれないので省略した部分もたくさんありますが、これを見るとゲーム木がどういうものか、おわかりいただけるのではないでしょうか。

ゲーム木は上から下に読んでいきます。図で状況を表している部分が「ノード」、「ノード」と「ノード」を繋いでいる線の部分が「エッジ」です。一番上のノードを「根ノード（root node）」と呼びます（図の赤い部分）。下の方にある緑の部分では、×が３つ並んでおり、後手の勝ちとなっています。勝敗がついているため、このノードはゲームの終着点であり、このノードから出ていくエッジはありません。このような末端のノードを「葉ノード（leaf node）」と呼びます。

囲碁・将棋・リバーシのようなゲームは、サイコロを使うようなゲームと違い、自分が手を選択すると、次の状況は確定します。（次の次の状況というのは、相手の手によって変わってきます。）サイコロを使うようなゲーム（すごろく等）では、例えばサイコロを1個振るか2個振るかによって次の状況が確定するかというとそうではなく、確率的に次の状況が決まります。確率的に状況が決まるタイプのゲームだと、ゲーム木で記述しようとしても複雑になりますが、囲碁や将棋やリバーシのように確率的でなく決定的に状況が決まるゲームでは、ゲーム展開をゲーム木で考えると考えやすいです。

途中で省略せず、全ての分岐を葉ノードまで展開したゲーム木のことを完全ゲーム木と呼びます。完全ゲーム木を書くことができれば、そのゲームがどんな風に展開していくのかを全て知ることができるので、そのゲームは先手必勝なのか、後手必勝なのかもわかりますし、実際に勝つための手順も完全に理解することができます。完全ゲーム木の葉ノードが多ければ多いほど、ゲーム展開の分岐が多い複雑なゲームであると解釈することができるため、完全ゲーム木の葉ノードの数をゲーム木複雑性と呼び、ゲームの複雑度の一つの指標とされます。
ちなみに、Wikipediaによると、3目並べのゲーム木複雑性は26,830だそうです。省略せずに書き切って、完全解析できる量ではありますが、このブログに乗せるには大きすぎる数ですね。これもWikipediaの情報ですが、オセロだと10の58乗、チェスだと10の123乗、将棋だと10の226乗、囲碁では10の400乗と見積もられるようです。ここまで複雑なゲームだと、完全ゲーム木を書いて完全解析するというのは、現実的ではないですね。

そのため、ゲーム木の考えは使いつつ、不完全なゲーム木でより正確な判断をすることが重要となります。ある局面で次に何を指すべきか、パッと有望な候補を絞り込み、その手が本当に有望なのかを、妥当であろう手の応酬である程度盤面を進めてみて、数手後の盤面がどちらにとって有利かという盤面の価値を正確に判断する。そのような能力が求められるわけです。

2. モンテカルロ法

さて、強化学習入門～これから強化学習を学びたい人のための基礎知識～ - Platinum Data Blog by BrainPad で紹介した通り、強化学習の問題を解くための方法の一つに、モンテカルロ法があります。
モンテカルロ法は、何らかの報酬が得られるまで行動をしてみて、その報酬値を知ってから、辿ってきた状態と行動に対してその報酬を分配していく方法でした。
この方法をゲーム木に対して適用すると、どうなるでしょうか。
3目並べのゲーム木も結構書ききるのは大変だとわかったので、ニムと呼ばれるゲームでゲーム木を書いてみましょう。

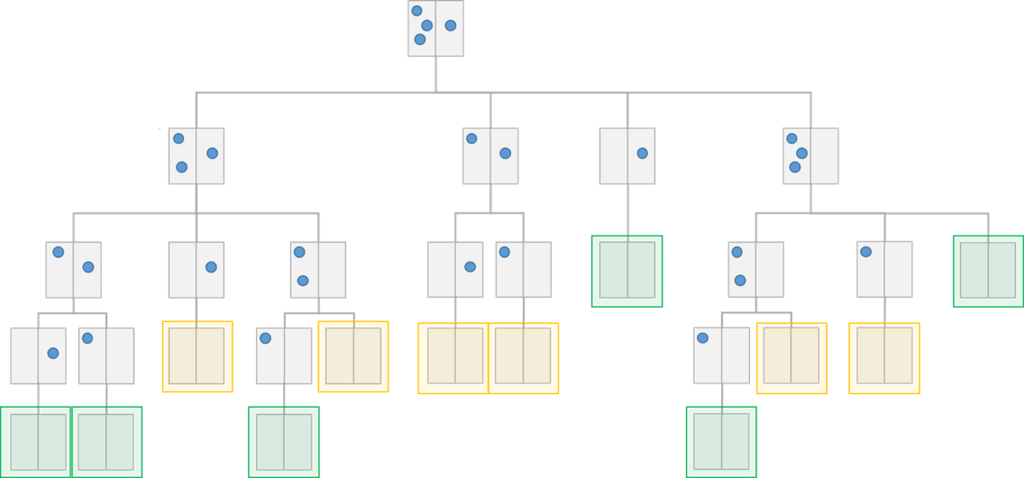
ここでのニムのゲームルールを説明すると、2人対戦で、プレイヤーは交互に、右左どちらかの石を1個以上の好きな数だけ取り除いていき、最後の石を取り除いたプレイヤーの勝ちとなります。ここでは、左に3個、右に1個の石がある状態を初期状態とします。
上記のゲーム木で、黄色で囲まれた葉ノードが先手勝ち、緑色で囲まれた葉ノードが後手勝ちのノードです。

では、完全にランダムに手を選択するという方策のもとで、モンテカルロ法で1,000ステップ回してみましょう。

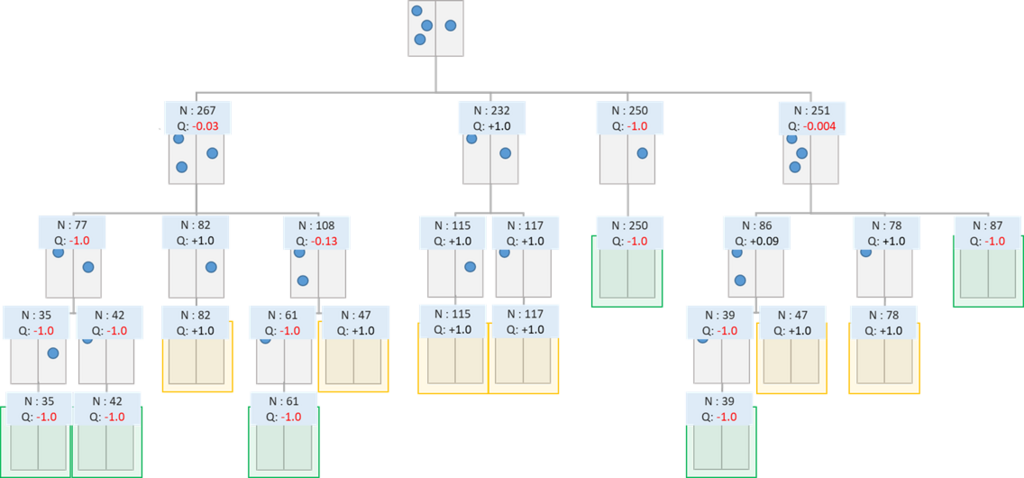
Nが選択した回数、Qが平均報酬です（先手が勝利した場合に +1 、後手が勝利した場合に -1 としています）。
最初の選択肢で、左から石を2個取り除き、左右1個ずつにする手（図の左から2番目の選択肢）が平均報酬が最大となっており、最善手を選択できることが確認できます。
しかし、例えば右から石を1個取り除き、左3個、右0個の状態にする手（図の一番右の選択肢）は、平均報酬がほぼ0となっています。実際には、左3個右0個の状態から後手が最善の手を選択すると後手勝ちなので、初手から左3個右0個の状態にする手の期待報酬は-1.0と推定されるのが望ましいです。これは、モンテカルロシミュレーションにおいて後手が最善の手を選択できておらず、完全にランダムに選択していることが原因です。

それでは、完全ランダムよりも良い方法はないでしょうか？その時点での平均報酬が高い手を選び続ける、という方法も思いつきますが、一般的にそううまくいきません。本当は勝てるはずの展開に進んでいたのに、途中でたまたま負けてしまった場合、その展開に進む手はその時点での報酬が -1 となり、以降その手が選ばれることがなくなってしまうためです。
平均報酬が高い手を選びたいが、平均報酬がまだうまく見積もれていない手は、ある程度見積もれる段階までは選びたい。とはいえ、見積もり精度を高めれば高めるほど試行数が必要となり、時間が無駄にかかってしまう。
このトレードオフに対して、理論的にある上界で無駄を抑えられるアルゴリズムとして、UCB（Upper Confidence Bound）というアルゴリズムが知られています。ゲーム木の探索にUCBを取り入れた手法が「Bandit Based Monte-Carlo Planning （Kocsis, Levente, and Csaba Szepesvári 2006）」という論文でUCT（UCB applied to trees）として紹介されました。UCTやそれと同様の枠組みの手法が、モンテカルロ木探索アルゴリズムと呼ばれています。

3. モンテカルロ木探索

モンテカルロ木探索は、5つの要素で構成されます（要素の表記はAlphaGoの論文*1に合わせています）。

Selection
Expansion
Evaluation
Backup
Play

1~4までが、頭の中で展開を色々シミュレーションしているのに該当し、5が実際の手の選択に該当します。

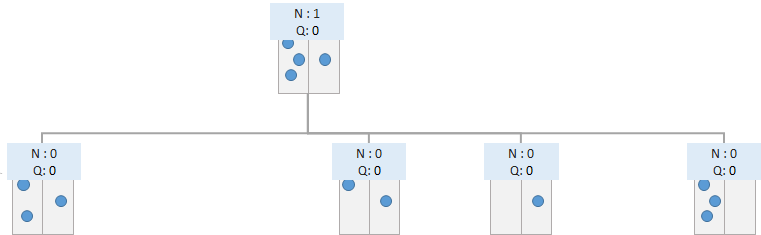
Selection

初期状態からどの手を選ぶか、モンテカルロ木探索で選択する手順を示します。先ほどニムの完全ゲーム木を書きましたが、囲碁や将棋では完全ゲーム木を書くことは現実的ではありませんので、モンテカルロ木探索の手続きの中でゲーム木を少しずつ展開していくこととなります。先ほどのニムの場合、初期状態からは4通りの選択肢があります。Qは今回は0で初期化していますが、乱数で初期化しても構いません。
頭の中で、一手動かしてみます。モンテカルロ木探索では、頭の中で動かす手として、以下の式が最大になる手を選択します。
$Q(s, a) + c(s, a)$

ここで、sは状態（＝ゲーム木のどのノードにいるか）、aは行動（=状態sにおいて可能な選択肢のうちの一つ）、
Q(s, a)は状態sにおいて行動aを取った時の価値（=期待報酬）、c(s, a)は状態sにおいて行動aを取ることのコスト関数です。c(s, a)は、Q(s, a)の見積もり精度に応じて、見積もり精度が低いほど大きく、見積もり精度が高いほど小さくなるような関数です。つまり、モンテカルロ木探索では、頭の中でどの手を選ぶかについて、基本的には推定している期待報酬が最大のものを選択するけれども、見積もり精度が低い手については下駄を履かせ、多少の期待報酬差なら期待報酬が最大以外の手を選んでみて、見積もり精度を上げる、という思想で手を選ぶことになります。

c(s, a)をどう設計するかについて、UCTでは以下が提案されており、この場合には理論解析がなされています。
$\displaystyle c(s, a) = C_{p} \frac { \sqrt{2log{n_{s}} }} {n_{s, a}}$

$n_{s, a}$ は（頭の中で）状態sから行動aを選択した回数、 $n_{s}$ は（頭の中で）状態sを訪れた回数です。
$n_{s, a}$ が小さい行動aほど、c(s, a)は大きくなります。
$C_{p}$ は正の値で、どの程度探索を重視するかを決定するハイパーパラメタとなります。

今回は、どの行動も選択回数が0なので、どの行動もc(s, a)が無限大となり、 $Q(s, a) + c(s, a)$ に差がつかないので、どれを選んでも問題ありません。仮に、一番左の選択肢が選ばれたとしましょう。

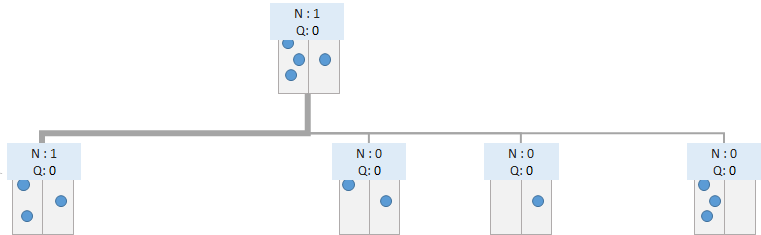
この時点でのゲーム木の葉ノードに到達しました。勝敗はついていないので、このノードから先のノードを展開することができます。
葉ノードに到達していない場合は、葉ノードに到達するまで、Selectionを繰り返します。

Expansion

モンテカルロ木探索では、ある時点でゲーム木の葉ノードに到達したとき、その葉ノードを訪れた回数が閾値以上となった場合に、ノードから先を展開します。閾値をいくつに設定するかはハイパーパラメータとなります。今回は説明を簡単にするため、2回訪れていたら展開することとします。
まだ1回しか訪れていないので、この段階では展開は行いません。

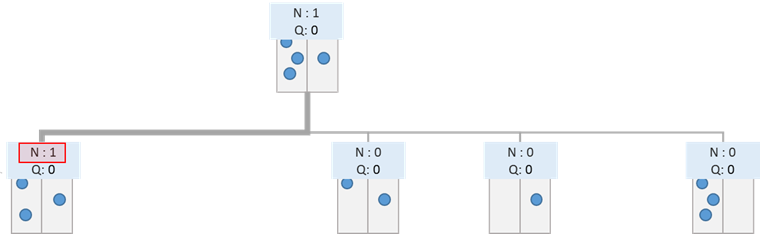
仮に、以下のように2回目に訪れた場合を考えてみましょう。

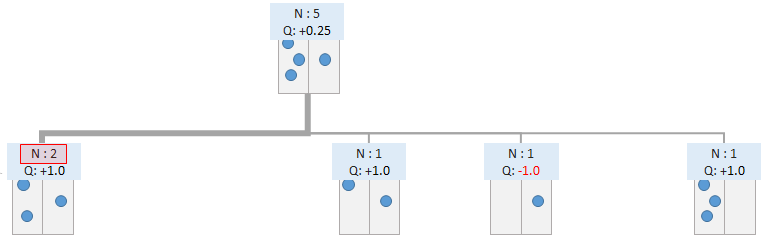
この場合には、閾値に到達したため、Expansionを行います。つまり、ノードから先を展開し、ゲーム木を拡張させます。

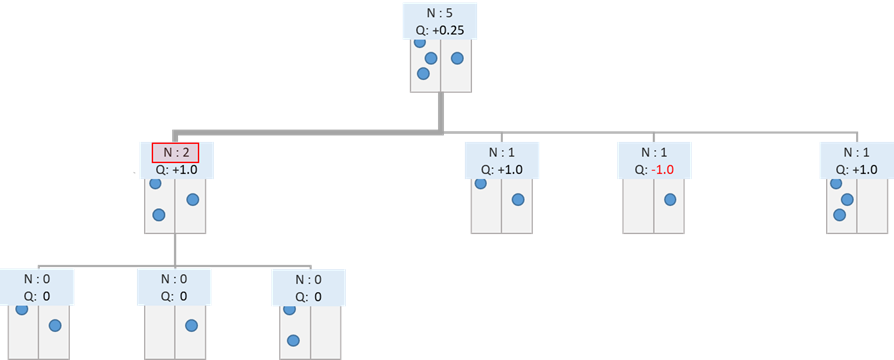
拡張した後は、Selectionに戻ります。
閾値を小さくするほど木は拡張されやすくなり、深く探索される反面、探索時間はかかってしまいます。閾値を大きくすればするほど、期待報酬の低い選択肢について探索が浅くなり無駄な探索が減る半面、有用な展開についても深い探索がされにくくなります。

Evaluation

ゲーム木の葉ノードから得られる報酬を評価します。モンテカルロ木探索では、Rolloutと呼ばれる方法で評価を行うことが一般的でした。（後述しますが、AlphaGoZeroやAlphaZeroではRolloutを行わず、別の方法で評価します。）
Rolloutでは、ゲーム木の葉ノード以降は、決着がつくまでランダムに手を進め、その勝敗をそのまま報酬とします。一様ランダムな方策とした場合、モンテカルロ法でやったのと同じく、本当は後手必勝だったとしても、Rolloutの結果としては先手の方が勝ちやすい状況も起こりえます。そのため、Evaluationの精度を高めるためには、一様ランダムではなく、有望な手を選びやすいようなサンプリングを行うことが有効となります。ただし、モンテカルロシミュレーションでは、実際の手を1手指すために何度も何度も頭の中でシミュレーションを回すこととなるため、Rolloutも何度も何度も行うこととなり、手を選択するために時間がかかると、モンテカルロシミュレーションにかかる時間が一気に増えてしまいます。AlphaGoでは、教師あり学習によって、プロと同じ手を当てるように学習した単純なモデルを構築し、その推定値に応じた確率で手を選択しながらRolloutを行っていました。

今回のRolloutでは、一様ランダムに手を選択することとして、Rolloutの結果先手が勝ったとしましょう。

Backup

得られた報酬の情報を記録します。今回のシミュレーションで訪れたすべてのノードについて、Rolloutで得られた報酬を記録し、期待報酬を更新します。これは強化学習のモンテカルロ法において、報酬が得られたタイミングで、辿ってきた行動と状態のペアに対してQ値を更新する手続きと同じものです。

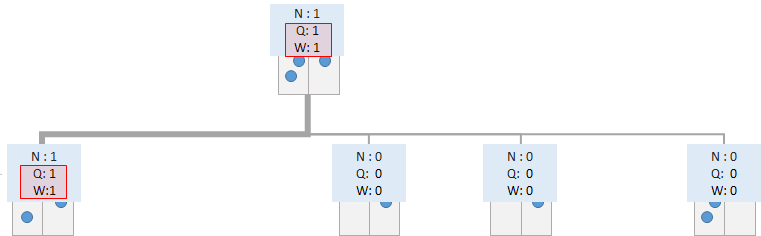
Backupが終わったら、根ノードに戻って、再度SelectionからBackupまでを繰り返します。

Play

Selection ~ Expansion ~ Evaluation ~ Backup の流れを何度も繰り返すことで、Q値を更新し、Q値の推定精度を高めます。そして、事前に決めていた試行回数だけSelection ~ Expansion ~ Evaluation ~ Backup の流れを繰り返したら、実際に着手する手を選択します。実際に着手する手の選択は、各行動のQ値または選択数に応じて確率的/決定的に選択します。
例えばAlphaGoでは、選択数が最も多い行動を実際の着手として選択します（Q値をそのまま使うよりも、外れ値の影響を受けにくいため。Selectionのロジックから、期待収益の高い行動は多く選択されます）。AlphaGoZeroでは、 $n_{a}^{1/\tau}$ に応じた確率で実際の着手を選択します。( $n_{a}$ は行動aの選択数、 $\tau$ は、どの程度探索を行うかのパラメタで、 $\tau=0$ だと選択数が最も多い行動を選択することとなり、 $\tau=1$ だと選択数に比例する確率で実際の着手を選択することとなります。 $\tau \to \infty$ で一様ランダムとなります。

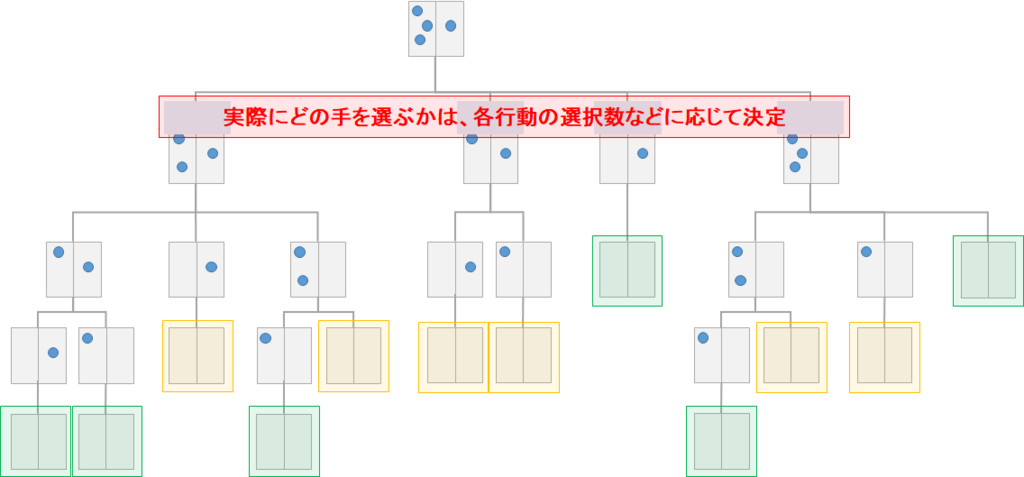
以上が、基本的なモンテカルロ木探索の流れとなります。1手着手するために、Selection ~ Expansion ~ Evaluation ~ Backup の流れを何回もシミュレーションして決めることになるので、回数を増やせば増やすほど精度は増しますが、時間がかかります。

以上で、モンテカルロ木探索を行うための知識は一通り説明しました。深層学習を組み合わせなくとも、Rolloutの際の方策が一様ランダムであろうとも、簡単な問題であればそこそこ良い手を着手できます。
ちょっと複雑なゲームになってくると、Rolloutの際に一様ランダムだとさすがに評価の質が悪くなります。（理論的には試行回数について極限を取れば正しい評価値に収束するのですが、実際には有限回のシミュレーションですので。）そのため、Rolloutの際にどの手を選ぶかについても、良さそうな手を選ぶよう、ルールベースなり、機械学習なりで対応する必要があります。

4. モンテカルロ木探索（AlphaZeroバージョン）

以上が基本的なモンテカルロ木探索ですが、モンテカルロ木探索にはいくつか弱点があります。
特に、Rolloutを用いていることに起因する弱点があります。

Rolloutの着手選択で良い手を選べる確率が高いほど少ない試行数で精度良く手の良し悪しを評価できるが、Rolloutは何度も何度も実行される処理なので、Rolloutでの着手選択を高精度にしようとして着手選択の実行時間が増えると処理全体にかかる時間が増大するため、高精度にしづらい。
囲碁やリバーシのように、徐々にマスが埋まっていきゲームが終了するゲームだとRolloutで勝敗を判断できるが、将棋やチェスのようなゲームだと、Rolloutで勝敗がつかないケースが多発する。（Rolloutは確率的に手を選んでいるため、ゲームによっては無駄な手の応酬に陥ってしまい決着がつかないことがある）

AlphaGoZeroやAlphaZeroの凄さは色々ありますが、

人間の対局データを一切必要としない（AlphaGoでは使っていた）
feature engineering を必要としない（AlphaGoでは多少していた）
ネットワークを複数必要とせず、一つのネットワーク（AlphaGoでは４つものネットワークを用いていて複雑だった）
Rolloutを必要としないモンテカルロ木探索アルゴリズムである

というのが主な点だと思います。その中でも、人間の対局データを一切必要としないという点が、衝撃的な謳い文句として、様々なメディアで取り上げられています。
ですが、技術的な視点で見ると、Rolloutを必要としないモンテカルロ木探索アルゴリズムであるという点が最も重要だと私は考えています。ネットワークを複数必要としないのも、人間の対局データを用いずに済んだのも、Rolloutをしなかったからだと考えられます。
AlphaGoZeroのアルゴリズムがRolloutを必要としなかったために、将棋やチェスなど、今まではモンテカルロ木探索と相性の悪かったゲームにもモンテカルロ木探索が適用できるようになったのは本当に凄いことだと思います。

それでは、AlphaGoZeroおよびAlphaZeroについて、アルゴリズムの骨格となる部分を説明します。
（AlphaZeroはAlphaGoZeroを一般化したアルゴリズムなので、骨格となる部分は同じです）

AlphaGoZeroおよびAlphaZeroでは、大きく下記２つのタスクを行っています。

Self-Play
Neural Network Training

Self-Playでは、モンテカルロ木探索により手を決定し、自分自身と何度も戦わせます。
AlphaGoZeroやAlphaZeroでは、Selectionでの $Q(s, a) + c(s, a)$ の式において、
$\displaystyle c(s, a) = C_{p} P(s, a) \frac { \sqrt{\sum_{b} n_{s, b}}} {1 + n_{s, a}}$
としています。ここで、P(s, a) は、ニューラルネットワークの出力であり、状態sにおいて行動aを着手する確率の推定値です。単に探索数に応じて下駄を履かせるだけでなく、P(s, a)が入ることで、ニューラルネットワークでの予測確率が高い手をより選択しやすくし、予測確率が低い手はほとんど選択しない、というさらに効率的*2な方法となっています。
Self-Playではニューラルネットワークの学習はされません。Self-Playは、ニューラルネットワークの学習に使うための棋譜データを作るためのタスクです。

Neural Network Trainingでは、Self-Playから得られた棋譜データを用いて、ニューラルネットワークの学習を行います。図を見てわかるように、ネットワークは一つです。ネットワークの入力は盤面の状態sで、出力は２つあります。一つの出力は、その状態からどの手を選択すべきかという、各手の着手確率です。これはpolicy networkにあたります。もう一つの出力は、その状態の価値、つまりその状態で当該プレイヤーが勝つ確率です。これはvalue networkにあたります。
policy network では、Self-Playでモンテカルロ木探索をした結果得られた、各手の着手確率を正解データとして、モンテカルロ木探索の結果との誤差が小さくなるように学習します。value networkでは、Self-Playの結果、その状態の後最終的にどちらが勝ったのかという勝敗の情報を正解データとして、誤差が小さくなるように学習します。

Self-Playは、ネットワークのパラメータを固定すれば、Neural Network Trainingとは独立にデータ作成できますし、Neural Network Trainingも、学習に使うデータを固定すれば、Self-Playとは独立にネットワークを学習できます。そのため、論文では非同期にこの2つの処理を行っています。

Self-playの中で、モンテカルロ木探索を用いますが、AlphaGoZeroでは以下のような手順となっています。普通のモンテカルロ木探索との違いとしては、Expand and evaluateです。SelectやBackup、Playについては、QやUの定義の違いを無視すれば普通のモンテカルロ木探索と同じです。

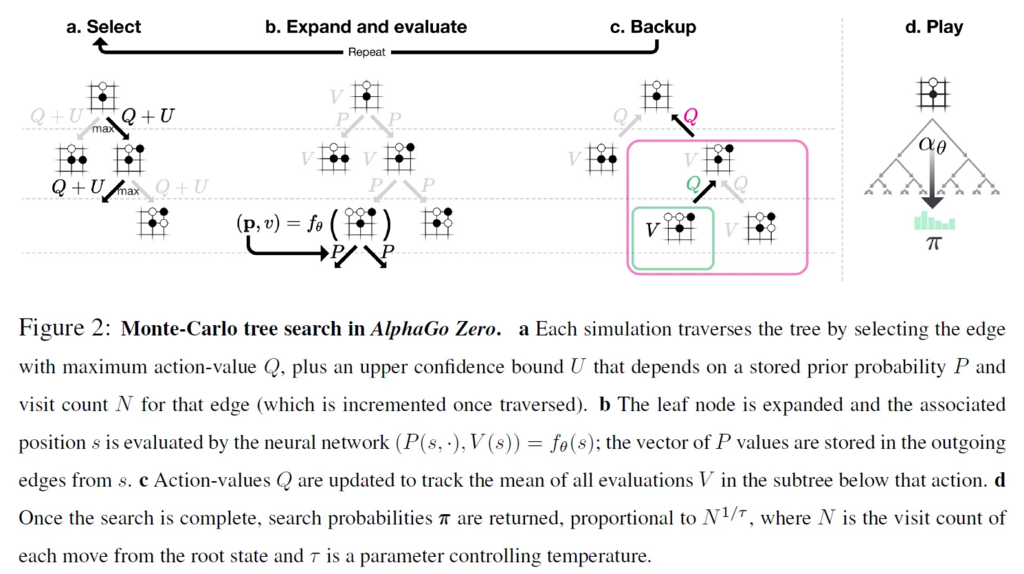
Expand and evaluate 、特にevaluateが、AlphaGoZeroの優れた工夫となっています。モンテカルロ木探索ではrolloutによって評価を行っていましたが、AlphaGoZeroでは、葉ノードの評価にrolloutを用いず、value networkで推定された価値関数をそのまま報酬としています。これにより、rolloutをするよりも時間を短縮できますし、rolloutでは勝敗が着かないようなゲームにも適用可能です。

ところで、Self-PlayとNeural Network Trainingにより、なぜ強くなることができるのでしょうか。多少乱暴ですがイメージを説明します。
Self-Playの中では、モンテカルロ木探索では、どの手を深く読むかをpolicy networkの出力を参考に決めながら、先読みを行います。先読みの中で、value networkにより局面判断を行っています。
Neural Network Trainingでは何を学習しているのでしょうか。value networkは、実際の勝敗をもとにして、局面の良し悪しを学習していると言えます。policy networkは、その局面においてどの手がどのくらい有望かを学習していると言えます。将棋や囲碁をある程度やったことがある人であれば、その局面で良さそうな候補手が一目でいくつか浮かぶと思いますが、policy networkの出力も、「一目どの手が良さそうか」という直感に当たると解釈できるのではないでしょうか。
そして、Self-Playの中でモンテカルロ木探索を行うことにより、深い読みを入れたうえでどの手が良さそうかを評価します。直感が外れていた場合には、モンテカルロ木探索により深い読みを入れることで、モンテカルロ木探索から得られるpolicyはpolicy networkから得られるpolicyよりも改善されます。そしてその改善されたpolicyでpolicy networkを学習することで、直感を鍛えていると解釈できます。

以上が、AlphaGoZeroおよびAlphaZeroのアルゴリズムの骨格部分となります。論文ではこの骨格の上に、速度を向上させる工夫、学習をうまく進めるための工夫、ハイパーパラメータの最適化など、様々なテクニックが取られています。細部まで論文に記載されていますので、詳細なテクニックを知りたい方はぜひ論文を読んでみてください。

それでは実際に、骨格部分だけを実装し、AlphaGomokunarabeZeroを作ってみます。
五目並べの競技バージョンは連珠と呼ばれ、様々な禁じ手があるのですが、今回は一切の禁じ手無しのルールです。三々でも四々でも長連でもなんでもOKです。
なお、五目並べレベルでも、結構時間がかかります……。そのため、対局データのバッファサイズや各学習に用いるデータサイズなどはかなり小さくして実験しています。
また、論文と違い、すでに石のある場所も選択できる設定にしています。ただし、すでに石がある場所を選択した場合は、即座に反則負けとしています。これにより、すでに石がある場所には置けないというルールも自動で学習することを期待しています。

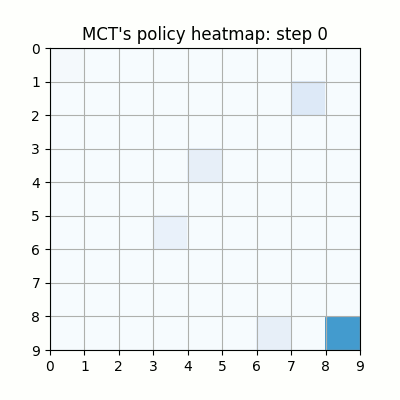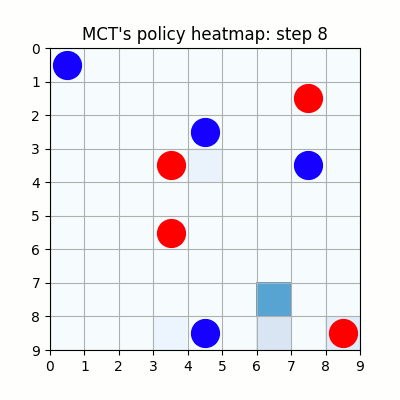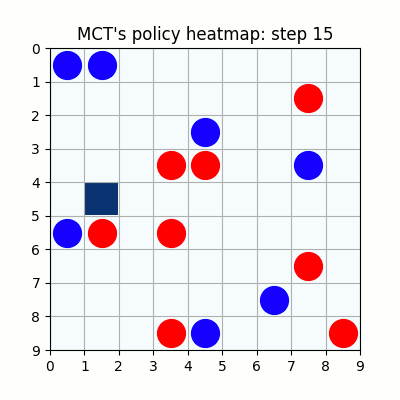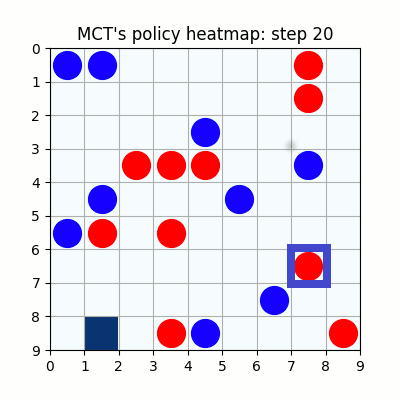
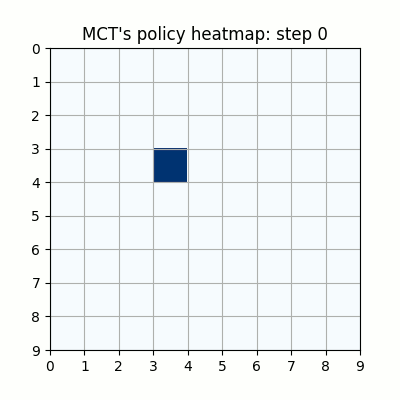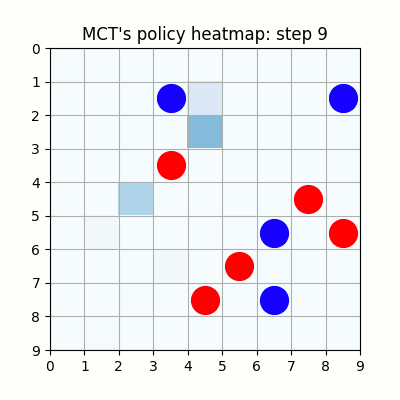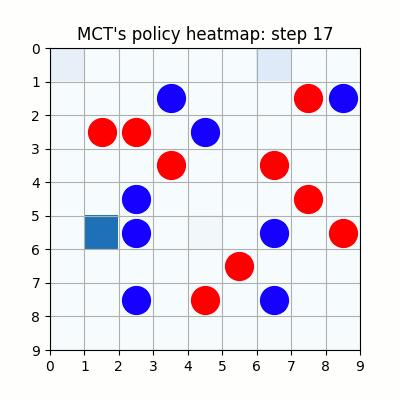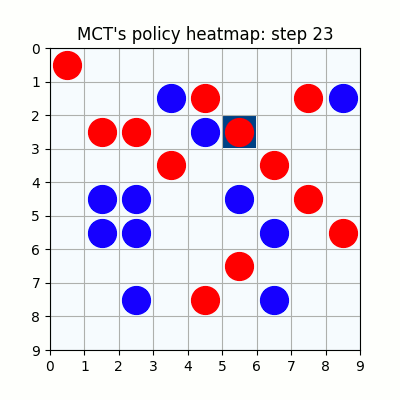
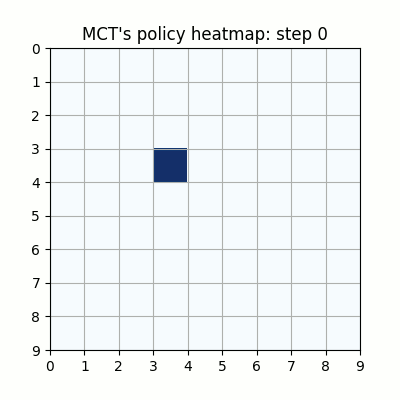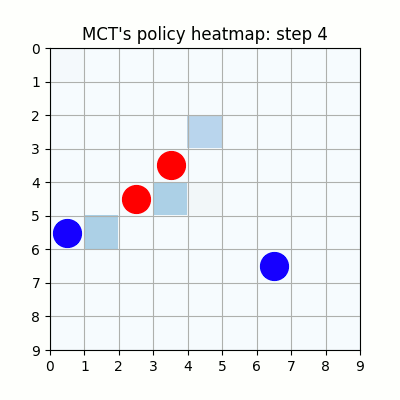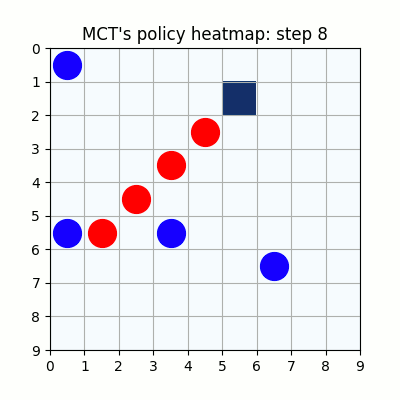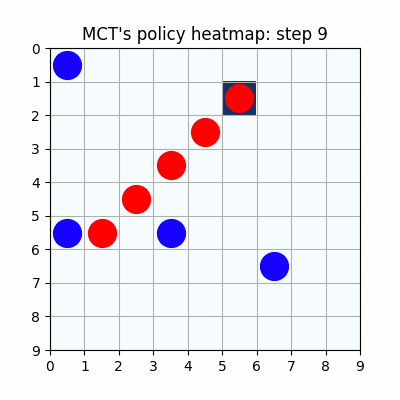
上記は最初の試行です。先手が赤色、後手が青色の丸で表示しています。マスに色がついているのは、モンテカルロ木探索の結果得られた、各マスを選択する確率をヒートマップで表したものです。
ネットワークの重みが全く学習されていない状態ですが、モンテカルロ木探索により石のないマスを選択するように色がついていることがわかります。確率的に手を選択しているので、必ずしも色の濃いマスを選択するとは限らず、今回は20手目で後手が反則負けとなっています。

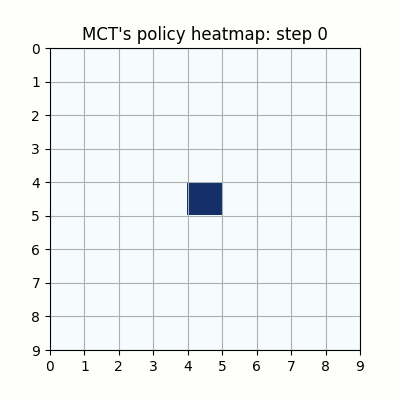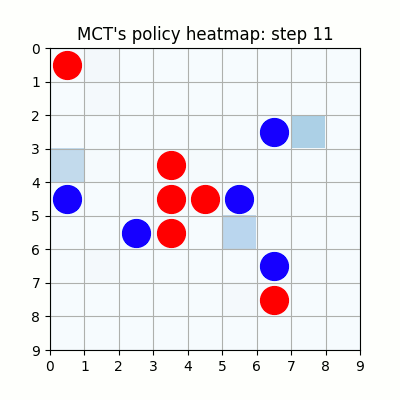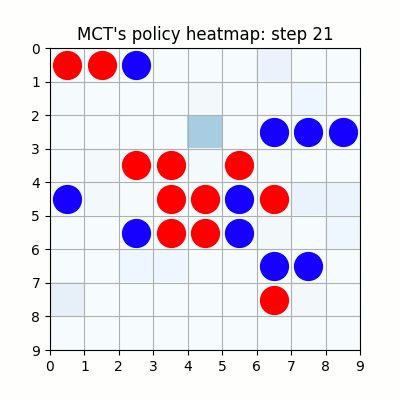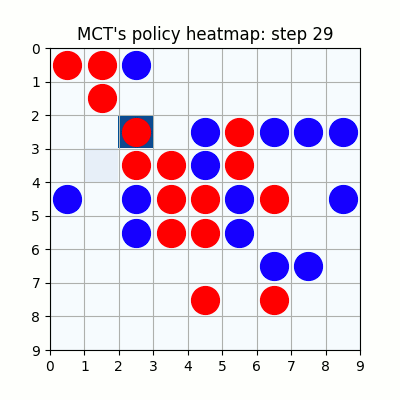
上記は100試行目です。まだまだ無茶苦茶ですね。21手目で赤色がリーチを作りますが、青色はそれを防げていません。そのまま23手目で赤色が勝っています。

2000試行付近です。まだまだ下手ですが、21手目で青がリーチを掛けた時、22手目で赤がそれを防げています。27手目で赤がリーチをかけた後、青が防げずに29手で赤が勝っていますが、28手目、リーチを防げる場所の色が最も濃くなっており、どうやらリーチを防ぐ概念が学習されたようです。

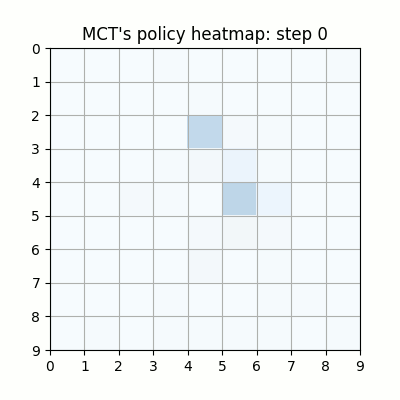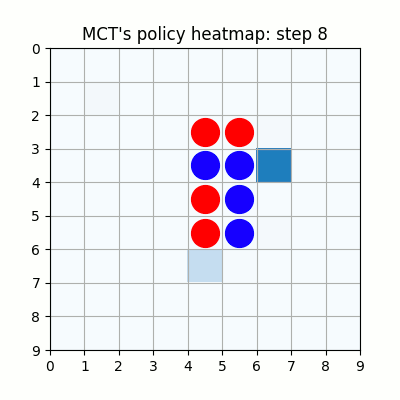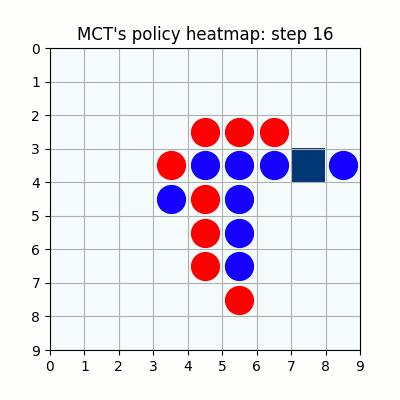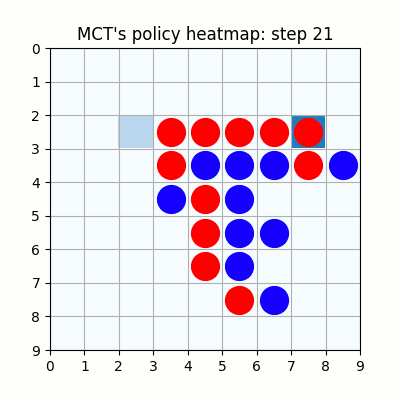
7000試行付近です。おかしい手もありますが、それっぽい戦いを繰り広げています。学習を高速化させるための工夫を実装しなかったため、GPU1枚で、この段階で2週間くらいかかっています。

10000試行付近です。赤色ばかりが勝ち、何をやっても一向に勝てなくなった青色はゲームを諦めてしまいました。
連珠には様々な禁じ手がありますが、今回は一切の禁じ手がありません。このサイズでも禁じ手がなければ先手必勝のゲームなのか、あるいは引き分けに持ち込むことができるのかを、私はわかっていないため、本当に青色はどこに打とうが結果が変わらないのか、それとも学習時のパラメタ設定が悪いせいでこのような結果になってしまったのかは定かではありませんが、極めて先手有利なゲームであることには間違いありませんので、挙動には納得はいきます。

実際にAlphaZeroの手法をビジネスに活かすためには、問題設定として確率的な状態遷移を許容するなど、拡張しても機能するかを考える必要があるでしょう。また、実行時間をいかに短縮するかが極めて大きな問題に感じます。

5. おわりに

今回は、強化学習に関係の深い、モンテカルロ木探索について簡単に紹介しました。興味を持たれた方は、下記のサーベイ論文などを参照いただくと、UCBについての説明のような基本的な内容がもう少し詳しく書かれていますし、様々なバリエーションや拡張について知ることができますので、読んでみてはいかがでしょうか。
Browne, Cameron B., et al. "A survey of monte carlo tree search methods." IEEE Transactions on Computational Intelligence and AI in games 4.1 (2012): 1-43.