トップ > まなぶ > 画像分類手法を用いた時系列分類手法とKaggle Code輪読会のご紹介

画像分類手法を用いた時系列分類手法とKaggle Code輪読会のご紹介

まなぶ

本記事は、当社オウンドメディア「Doors」に移転しました。

約5秒後に自動的にリダイレクトします。

ブレインパッドでは進化の激しいデータ分析業界で最新情報をキャッチアップしていくため、様々な勉強会が社内で開催されています。その中のKaggle Code輪読会について、その目的や活動内容、実際に発表された内容をご紹介します。


こんにちは。アナリティクスサービス部の諸橋と申します。
この記事ではブレインパッド社内で行われている勉強会の一つである「Kaggle Code輪読会」についてご紹介します。
また、輪読会で紹介されたKaggle Code（※データ分析プラットフォームKaggleに投稿された分析コードのこと）とその議論の内容についても紹介します。

今回紹介するKaggle Codeはセンサーデータとして取得された時系列データをグラフ化し、そのグラフに対して画像分類を行うことで元々の時系列データの分類を行うという手法です。
技術的な内容と併せて、日々の勉強会を通してお互いに切磋琢磨し合うブレインパッドのデータサイエンティストの雰囲気も感じ取っていただければ幸いです。

Kaggle Code輪読会について

データ分析プラットフォームであるKaggle内に投稿されたCode（※Kaggleにおいて過去はkernel、notebookと呼ばれていました）を主な題材とするブレインパッドの社内勉強会の一つです。
毎回発表者が興味を持ったKaggle Codeを輪読会でシェアし、Codeの内容について参加者全員で議論する、という流れで進みます。
目的は「個々の分析手法の概要をサラッと知る」ことです。
「特定の領域について深く、詳細に理解する」ことより、分析コンペ等で使用された手法や最新のニーズをパパっと捉えることに重点を置いています。

もちろん、「特定の領域について深く、詳細に理解する」ことを軽視しているわけでは無く、こちらは別の様々な勉強会で実現されています。
例えば、最近ブレインパッドが全社的に力を入れている数理最適化領域は盛んに勉強会などが行われており、当プラチナブログでも多数の 最適化ブログ が書かれています。
ご興味のある方はそちらもご覧ください。

Kaggle Code輪読会は社内勉強会の中でも長続きしている勉強会の一つで、調べてみると最初の発表が2019年5月でした。
2年以上続いているということで私もびっくりしています。
長続きしている理由は、多種多様な分析を依頼される受託分析という業務の特殊性と、実際に使用可能なコードも交えてパパっと手法を知ることができるという手軽さがマッチしたためではないかと個人的には考えています。
参加者は受託分析業務に携わるデータサイエンティストが最も多いですが、最近は教育講座を主催するデータ活用人材育成サービス部の方や、データ分析基盤などの構築を主に行うデータエンジニアリング本部の方も参加され、参加者の多様性が増しています。
参加者の多様性が増すにつれ、発表内容も分析コンペのCodeを題材にした分析手法についてだけでなく、各種AutoMLサービスのエンジニア視点での比較など、分析に関わる様々な知見が部署を横断して蓄積されるようになってきました。

Kaggle Code輪読会は今後も進化し続けるデータ分析業界のトレンドにブレインパッドが追随するための大きな原動力となるでしょう。

今回の記事では、過去に私が実際にKaggle Code輪読会で発表した内容を活動内容の例としてご紹介します。

余談ですが、ブレインパッドには社内勉強会をスムーズに行うための仕組みが整備されており、勉強会の告知や参加がとてもやりやすくなっています。
詳細は こちらのPodcasts で紹介されていますので、ぜひ聞いてみてください。

リカレンスプロット+CNNによる時系列分類

さて、ここから実際に勉強会でシェアしたKaggle Codeの詳細について説明します。
シェアしたCodeはこちらです。
RecuPlots and CNNs for time-series classification

こちらのCodeでは画像分類手法を用いて時系列データの分類を行う方法について解説されています。

「時系列データの分類」というタスクは、例えば人に付けた加速度計センサーなどの時系列データから、その人が走っているか歩いているか分類する、といったような問題をイメージしていただければ分かりやすいかと思います。

「時系列データで画像分類？」と頭に疑問符を浮かべる方もいらっしゃるかもしれません。私はそうでした。

種明かしを先にしてしまうと、時系列データ→グラフ化→グラフ画像に対して画像分類→時系列データの分類、という流れで時系列データを分類するという手法です。

今回紹介するCodeではリカレンスプロットと呼ばれるグラフ化手法でグラフを作成し、一般的なCNNで画像分類を行っています。
以降ではまずリカレンスプロットというグラフが何を表しているかを説明した後に、今回用いるデータの詳細とリカレンスプロットの応用方法を説明していきます。

リカレンスプロットについて

リカレンスプロットとは時系列データ \boldsymbol{x}(t) について、異なる時点 i, j において \boldsymbol{x}(i) と \boldsymbol{x}(j) の値がほぼ等しい時にグラフ上の座標 (i, j) に点を描画するプロットです。
数式で表現すると以下のようになります。 RT(i, j) が 1 なら点 (i, j) に点を描画し、0 なら点を描画しないことを表しています。

\displaystyle RT(i, j) = \theta (\epsilon - || \boldsymbol{x}(i) - \boldsymbol{x}(j) ||)

ここで、 \theta は ヘヴィサイドの階段関数 、 \epsilon は値が等しいか否かを判定する閾値、 ||\boldsymbol{x}|| は \boldsymbol{x} のノルムを表します。

数式で書くと小難しいですが、一次元の時系列を例に図で描くと以下のようにシンプルなプロットを表していることが分かります。

1次元時系列データのリカレンスプロットの例

紹介Codeでは例として、ランダムノイズと正弦関数のリカレンスプロットが描かれています。
リカレンスプロット RT(i, j) を生成する関数を以下に引用します。
閾値 ε の範囲内であれば値が等しいと判定されるので、リカレンスプロットは点 (i, j) 周辺は点が密になる疎密で表されるグラフとなります。
コードではノルムの最大値を steps に切り捨て、プロットを見やすくしています。
（コードはRecuPlots and CNNs for time-series classification より引用 ）

#modified from https://stackoverflow.com/questions/33650371/recurrence-plot-in-python
def recurrence_plot(s, eps=None, steps=None):
    if eps==None: eps=0.1
    if steps==None: steps=10
    d = sk.metrics.pairwise.pairwise_distances(s)
    d = np.floor(d / eps)
    d[d > steps] = steps
    #Z = squareform(d)
    return d

fig = plt.figure(figsize=(15,14))
random_series = np.random.random(1000)
ax = fig.add_subplot(1, 2, 1)
ax.imshow(recurrence_plot(random_series[:,None]))
sinus_series = np.sin(np.linspace(0,24,1000))
ax = fig.add_subplot(1, 2, 2)
ax.imshow(recurrence_plot(sinus_series[:,None]));

ランダムノイズ（左）と正弦関数（右）のリカレンスプロット。RecuPlots and CNNs for time-series classification より引用

図を見れば分かるように、ランダムノイズの方（左）は特にプロットに傾向は見られませんが、正弦関数（右）は点が密である部分が周期的に並んでいます。
これは正弦関数の周期性を反映した結果です。

さて、リカレンスプロットが何者かは分かりましたが、これが描けると何が嬉しいのでしょうか？
正弦関数の例から、リカレンスプロットは時系列データの周期性を表現したプロットであることは想像できます。
周期性を表現したプロットと言えばフーリエ変換などを用いたスペクトルが思いつきます。
これらスペクトルとリカレンスプロットの違いとして、紹介Code内では次のように述べられています。

A typical approach is to convert the time-series to a spectrogram.
This is disadvantageous since in a spectrogram it matters where an effect appears in contrast to CNNs where it is assumed that a feature is of the same kind,no matter where in the picture it is. The usage of recurrence plots as visualization of the recurrence structure of a time-series is hence advantageous. 

私の拙い英語力で意訳するならば、
「スペクトルはグラフの特定の一部に時系列の特徴が現れる。しかし、CNNでは画像全体がクラスを特徴づける構造を持つことを仮定している。そのため周期構造に特化した可視化としてはリカレンスプロットの方が有利である。」
といった感じでしょうか。

CNNでは画像全体に共通のフィルタをかけてから学習します。そのため、画像（グラフ）の特定の一部のみに時系列の特徴が表れるスペクトルよりも、画像全体に時系列の特徴が表れるリカレンスプロットの方がCNNと相性が良い、ということだと思われます。

もう一つ、リカレンスプロットの特徴を挙げます。
リカレンスプロットは数理物理学の研究対象であるカオス理論の研究でも用いられます。そこからの結果をご紹介します。

以下に様々な時系列データのプロットとリカレンスプロットを表した図を引用します。
左から白色雑音、2つの周波数による高調波発信、線形傾向を持つカオスデータ（ロジスティック写像）、自己回帰モデルのデータとなっています。

Wikipedia:リカレンスプロット より引用

白色雑音（一番左）と線形傾向を持つロジスティック写像（左から3番目）や自己回帰モデル（一番右）のリカレンスプロットに着目すると、ともにランダム性を持つ時系列データであるにも関わらず、リカレンスプロットには明確な違いが表れています。
白色雑音のリカレンスプロットには特徴が見えないのに対し、線形傾向を持つロジスティック写像や自己回帰モデルのリカレンスプロットには格子状の特徴が見て取れます。

白色雑音と線形傾向を持つロジスティック写像、自己回帰モデルの大きな違いは、後者2つはデータがただのランダムではなく、あるルール（方程式）に基づいて生成されているという点です。
このようにリカレンスプロットは「データを生み出す構造を反映した画像である」と言えるでしょう。
（より専門的な言葉を使うならば、リカレンスプロットは時系列データを生成する力学系の 位相空間 の構造を反映している、と言えます。）

今回用いるデータについて

リカレンスプロットが何者なのか分かった所で、実データへの応用例について説明を進めます。

紹介CodeではKaggle Datasetsにアップロードされているデータを題材としています。
Kaggle Datasetsには様々なデータがアップロードされており、分析の題材とすることができます。
ただし、データごとにライセンスが異なるので公開時は注意が必要です。

紹介Codeで用いられているデータは MotionSense Dataset : Smartphone Sensor Data - HAR です。（詳細については末尾の Citation をご覧ください。）

スマートフォン搭載のセンサーの時系列データを用いてスマートフォンを持った人の運動の状態を分類することが本データセットの課題です。
このような人間の姿勢や運動状態を推定するタスクは一般にHAR （Human Activity and Attribute Recognition）と呼ばれます。
運動の状態は、

  • 階段を降りる（Downstairs）
  • 階段を上る（Upstairs）
  • 座る（Sitting）
  • 立つ（Standing）
  • 歩く（Walking）
  • ジョギング（Jogging）

の7つとなっています。
一方、スマートフォンのセンサーデータからは以下の情報が時系列データとして与えられます。

  • 姿勢（roll, yaw, picthの3要素）
  • 重力加速度（x, y, zの3要素）
  • 角速度（x, y, zのそれぞれの軸まわり）
  • 加速度（x, y, zの3要素）

さらにユーザの属性として身長、体重、年齢、性別が与えられています。

データと前処理についてはgithub上でもまとまっているのでそちらもご参照ください。

github.com

上記リポジトリで挙げられている前処理によって、ユーザのセンサーデータと属性データを組み合わせ、以下のようなデータマートが作成されます。
以降の分析ではこのデータマートが使用されています。

https://github.com/mmalekzadeh/motion-sense より引用

本筋から少しそれますが、今回取得されたデータは人がスマートフォンを装着する位置、人が辿る経路などの条件を揃えた上で実験された結果です。
実際にセンサーデータを分析する際は「どのような位置に設置されたセンサーからどのようなデータが取得されているのか」という前提条件が非常に重要になります。
この前提条件の把握を疎かにしてしまうとそもそも不可能なことを実施しようとしてしまったり、間違った結論を導いてしまうことが起こってしまいます。
センサーデータに限った話ではありませんが、データ分析の際には「データがどのような状況で取得されたのか」について必ず気を配らなくてはなりません。

運動形態ごとのリカレンスプロット

では、紹介Code内で実際に上記のデータから作成された運動形態ごとのリカレンスプロットの例を見ていきましょう。
リカレンスプロットの作成方法はランダムノイズと正弦関数の例と同様なので割愛します。

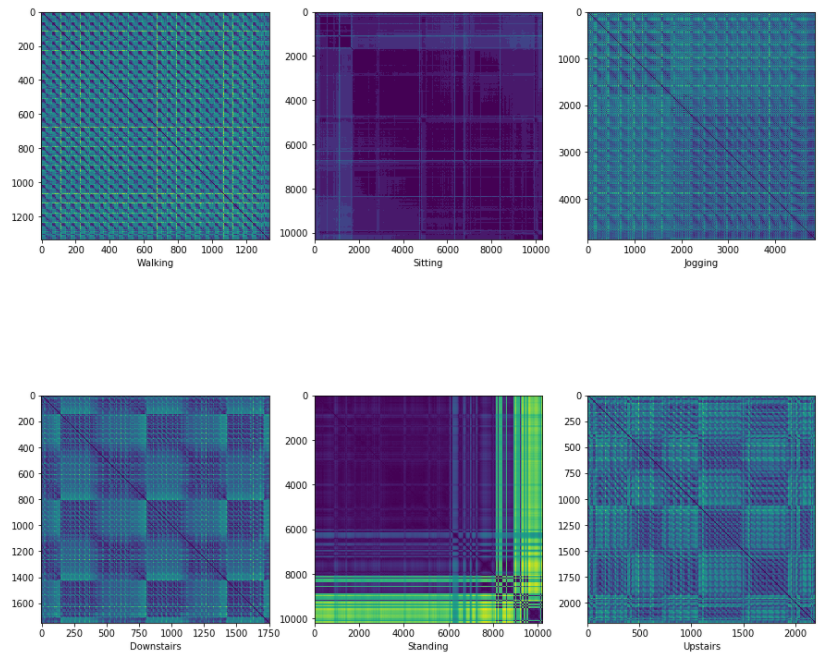
RecuPlots and CNNs for time-series classification より引用

運動形態ごとに特徴が分かれたプロットが得られています。
” Walking”と”Jogging”、”Sitting”と”Standing”、Downstairs”と”Upstairs”の3つの組でよく似たプロットになっていますね。
これは各々の周期的な構造が似ているからでしょうか。

“Walking”と”Jogging”に着目してみると、”Jogging”よりも”Walking”の方が密な部分が多くなっています。
これはジョギングよりも歩く方が運動の周期が短いことを反映しているのかもしれません。

ともあれ、運動形態ごとに異なるプロットが生成されたので、画像分類を行う価値はありそうです。

リカレンスプロットの画像分類

それでは、本題のリカレンスプロットの画像分類についてです。
といっても分類自体はCNNを利用した基本的なコードです。
以下、コードはすべて 紹介コード からの引用です。

前処理として、

  1. 運動形態のラベルを数値に変換し、
  2. 全時系列データから各々のリカレンスプロットを作成して、
  3. 各々のリカレンスプロットの画像サイズをそろえる。

ということが行われています。以下が前処理部分のコードです。

# convert folders to class labels
# downstairs/upstairs = 0,walking/jogging  = 1, standing/sitting = 2
class_translate = {"dws_1" : 0, "dws_2" : 0, "dws_11" : 0,  \
                   "ups_3" : 0, "ups_4" : 0, "ups_12" : 0, \
                   "wlk_7" : 1, "wlk_8" : 1, "wlk_15" : 1, \
                   "jog_9" : 1, "jog_16" : 1, \
                   "std_6" : 2, "std_14" : 2, \
                   "sit_5" : 2, "sit_13": 2}

#pre allocate arrays
x_train = np.zeros((384,32,32))
y_train = np.zeros(384)
c = 0
start = time.time()
for i in class_translate.keys():    
    print("Processing set " + i)
    for j in range(1,25):
        dat = recurrence_plot(pd.read_csv("../input/A_DeviceMotion_data/A_DeviceMotion_data/" + i +"/" + "sub_"+ str(j) + ".csv")[cols].values, steps=100)
        dat = resize(dat, (32,32),mode='constant')
        x_train[c,:,:] = dat
        y_train[c] = class_translate[i]
        c = c + 1
end = time.time()
print('Elapsed time:')
print(end - start)

CNNの画像分類モデルはKerasによって構築されています。

model = Sequential()
 
model.add(Convolution2D(32, (3, 3), activation='relu', input_shape=(1,32,32), data_format='channels_first'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Convolution2D(32, (3, 3),activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25)) 
model.add(Flatten())
model.add(Dense(64, activation='relu'))
#model.add(LeakyReLU(alpha=0.03))
model.add(Dropout(0.5))
model.add(Dense(3, activation='softmax'))

model.compile(loss='categorical_crossentropy',
              optimizer='adam',
              metrics=['accuracy'])

学習用のコードです。

#reshape to include depth
X_train = x_train.reshape(x_train.shape[0], 1, 32,32)
#convert to float32 and normalize to [0,1]
X_train = X_train.astype('float32')
X_train /= np.amax(X_train)
# convert labels to class matrix, one-hot-encoding
Y_train = np_utils.to_categorical(y_train, 3)
# split in train and test set
X_train, x_test, Y_train, y_test = train_test_split(X_train, Y_train, test_size=0.1)

model.fit(X_train, Y_train, epochs=200, batch_size=16,shuffle=True)

出力結果については最後の3 epochのみを引用します。

...
Epoch 198/200
345/345 [==============================] - 1s 3ms/step - loss: 0.0849 - acc: 0.9565
Epoch 199/200
345/345 [==============================] - 1s 3ms/step - loss: 0.0960 - acc: 0.9565
Epoch 200/200
345/345 [==============================] - 1s 3ms/step - loss: 0.1109 - acc: 0.9536

学習データについては約95%という高精度で運動形態を分類できることが示されています。
（テストデータの精度は紹介Code中で示されていませんでした。）

このように、リカレンスプロットに対して画像分類モデルを適用することで時系列データの分類を行えることが分かりました。

勉強会中の議論の内容

紹介Codeの内容は前節までで終わりですが、ここからは少し実際の勉強会で交わされた議論の内容を紹介します。
類似した研究内容や直近で行われた分析コンペとの関連についてはもちろん、実際の受託分析案件への応用の方法なども議論され、データ分析のビジネス活用に重きを置くブレインパッドらしい議論となりました。

受託分析案件への応用について

ブレインパッドにおける過去案件との関連から、「施設内のユーザの行動履歴から今回の手法でユーザ群の分類を行うことはできないか。」という議論が巻き起こりました。
特定の行動をとっているユーザに対してクーポンを発行するなど購買行動を後押しできないか、というアイデアです。
もちろん実際に可能かどうかは全くの未検証ですが、実際のビジネスに活かしやすい応用例かもしれません。
一つのアイデアとしてとても面白いものでした。

他分析コンペとの関連

この発表を行った少し前までKaggleで音声認識のコンペ（通称 鳥コンペ ）が行われていたこともあり、そのコンペで使われた手法との関連も議論されました。
このコンペでは音声データを分類する際、メルスペクトログラムという画像に一度変換し、CNNで画像分類を行うという手法が主に使われていました。

一度グラフに変換して画像分類というのは紹介Codeと同じ手法ですね。

コンペで用いられた手法との関連から、時系列データの圧縮による計算時間の短縮法まで議論されました。
リカレンスプロットは時系列を二回スキャンするため、計算時間が多大になる懸念があります。
そこでデータ圧縮の方法を用いることで時系列の特徴を保持しつつ処理を軽くする方法についても議論されたわけです。

類似手法について

今回の紹介手法の流れは時系列データ→グラフ化→画像分類という流れでした。
画像分類についてはCNNに限らず他のニューラルネットワークや事前学習モデルからの転移学習などでも可能です。

また、音声分類におけるメルスペクトログラムを初め、時系列データの特定の情報を捉えたグラフ化についても多数の類似手法が挙げられました。

medium.com

上記に挙げた以外にも、紹介手法とトポロジカルデータ分析との関連が指摘されるなど、有意義な議論が展開されました。

まとめ

今回はブレインパッド社内で行われている勉強会を紹介しつつ、例として勉強会で紹介した手法についても説明しました。
ブレインパッドの中の雰囲気を多少なりとも知っていただき、「時系列データの分類は時系列のグラフに対する画像分類でも可能」という知見を持ち帰っていただければ本記事としては大成功です。

なお、今回紹介した手法は音声分類の例を除き、私の知る限りビジネスの課題に対して確たる実績のあるものではなさそうです。
実際にビジネス課題を解決できるかは今後の検証が待たれるところかと思います。
それでも知見を広げ、様々な議論が巻き起こった点で社内勉強会としてとても良い内容になりました。

本記事からブレインパッドの互いに切磋琢磨し合う雰囲気を一端でも感じていただければ幸いです。

Citation

紹介したデータは以下から引用されています。
論文や記事などで使用される際は以下の情報を参考文献として挙げて下さい。

@inproceedings{Malekzadeh:2019:MSD:3302505.3310068,
author = {Malekzadeh, Mohammad and Clegg, Richard G. and Cavallaro, Andrea and Haddadi, Hamed},
title = {Mobile Sensor Data Anonymization},
booktitle = {Proceedings of the International Conference on Internet of Things Design and Implementation},
series = {IoTDI '19},
year = {2019},
isbn = {978-1-4503-6283-2},
location = {Montreal, Quebec, Canada},
pages = {49--58},
numpages = {10},
url = {http://doi.acm.org/10.1145/3302505.3310068},
doi = {10.1145/3302505.3310068},
acmid = {3310068},
publisher = {ACM},
address = {New York, NY, USA},
keywords = {adversarial training, deep learning, edge computing, sensor data privacy, time series analysis},
}


当社では、データサイエンティストを積極的に募集しています。 新卒採用・キャリア採用ともに、ご応募をお待ちしています！ www.brainpad.co.jp