本記事は、当社オウンドメディア「Doors」に移転しました。
約5秒後に自動的にリダイレクトします。
こんにちは。アナリティクスサービス本部の登内です。
当社では、データから価値を引き出すべく日々、様々なデータ分析に取り組んでいます。その中でも、来たるべき令和時代にブレイクするかも知れないテーマであるダイナミックプライシングへの取り組みも強化しています。今回は、ダイナミックプライシングの概要と定式化について紹介したいと思います。
この記事の目次は次のとおりです。
ダイナミックプライシングとは?
定義
ダイナミックプライシングとは簡単に言うと「収益増を目的に、同一商品の価格を販売期間中に変動させる価格設定戦略」と説明ができます*1。もともとは航空券、ホテル宿泊料などで実践されていた価格戦略ですが、近年ではアパレルECサイトなどでも取り組みが進みつつあります。ダイナミックプライシング先進国であるアメリカでは、適用範囲が拡大しつつあり、American AirlinesやMarriott Internationalのような航空・ホテル業界はもとより、Ticketmaster(チケット販売業)、AmazonやeBay(EC)、FedExやUPS(輸送業)、UberやLyft(配車マッチング)、General MotorsやFord Motor Company(自動車製造業)など様々な企業でダイナミックプライシングの試みがなされています。
メリット・デメリット
ビジネス科学の世界では、わずかな値上げであってもそのことがもたらす利益増は大きいことが指摘されています。例えば、ある記事によると「平均的な企業では」、「販売量が減らないと仮定した上で、価格を1%引き上げた場合、営業利益は11.1%も改善する」そうです*2。
この話から、需要が大きくて価格を上げられる状況で適切に値上げすることができれば利益に大きなインパクトをもたらす可能性があることがわかります。また、逆に在庫が余剰気味な状況の中で、値下げが必要な局面であっても、売り切る範囲内でできるだけ高く販売することが利益の確保にとって有効であることもわかると思います。
ダイナミックプライシングでは、販売期間中に何度も価格を変更=最適化するので、需給の状況によっては大きな収益増をもたらす可能性があります。ある記事ではダイナミックプライシングによって、「収益と利益をそれぞれ最大8%と25%向上させることができる」と述べられています*3。このように、大きな収益増が期待できる点が、ダイナミックプライシングのメリットと言えます。
一方、消費者の立場からは、ダイナミックプライシングにより需要の高い時期に価格が上がってしまうのは、あまり嬉しい話ではありません。売り手側がやり方を間違えれば、消費者からの反感を招きかねず、ダイナミックプライシングを実施する上でのリスクとなり得ます。この点は、ダイナミックプライシングのデメリットと言えるでしょう。
ダイナミックプライシングを適切に実践するためには、実際の需要・供給に関するデータを収集・分析し、統計やAIを活用して価格を最適化する仕組みを構築する必要があります。そのため、データ分析企業である当社が、ダイナミックプライシングの実現に強みを発揮できると考えています。
この記事では、以降、ダイナミックプライシングの定式化の簡単な一例をご紹介します*4。
定式化
問題設定
ここでは、「初期在庫有限、在庫の補充なし、販売期間有限」の場合の次のような問題設定について考察します*5。
- 販売商品の初期在庫数は有限であらかじめ決まっている。
- 販売期間は有限で、在庫品は販売終了時点で価値を失う。
- 売り手は、商品の価格を販売期間中に任意に変更できる。
- 買い手(顧客)は店舗に到着し、価格を参照した上で購入するか否かを決定する。ここで、顧客の到着と購買決定は確率的な事象とする。
- 競合品は売上に影響を与えない(話を単純にするための仮定)。
この設定は、先程述べた、航空券、ホテル、スタジアム座席などの例(を単純化したもの)とみなすことができます。
定式化
初期在庫と販売期間について、次を仮定します
- 初期在庫数をcとする。cは有限の値とする。
- 販売期間
(閉区間)を微小なT個の時間区間に等分割し、最初の時間区間を
、次の時間区間を
と順次番号付けする(販売終了直前の時間区間は
になる)。
すなわち、。時間区間は価格意思決定の時間刻みに合わせる。

顧客の到着数は確率的であるとします
- 期間
での顧客の期待到着数を
とする。
顧客の購買決定について、各顧客は、考察対象商品に対する「留保価格」(その商品を買っても良いと考える価格の上限値)を持っているとします。留保価格がいくらかは顧客によってまちまちで、確率的に分布するものとします;
- 期間
での顧客の留保価格
の分布関数を
とする。
- このとき、販売期間
に価格
で販売したとき、到着した顧客が商品を購入する確率は
となる。
このように仮定すると、設定価格での期間
における期待収益は
となります。
最適化
このように定式化すると、販売期間全体での累積期待収益が最大となる販売価格の列
を求めることができます。最適な販売価格
を求めるアプローチの一つは動的計画法によるものです。
- 初期在庫
、販売期間
で得られる最大総収益を
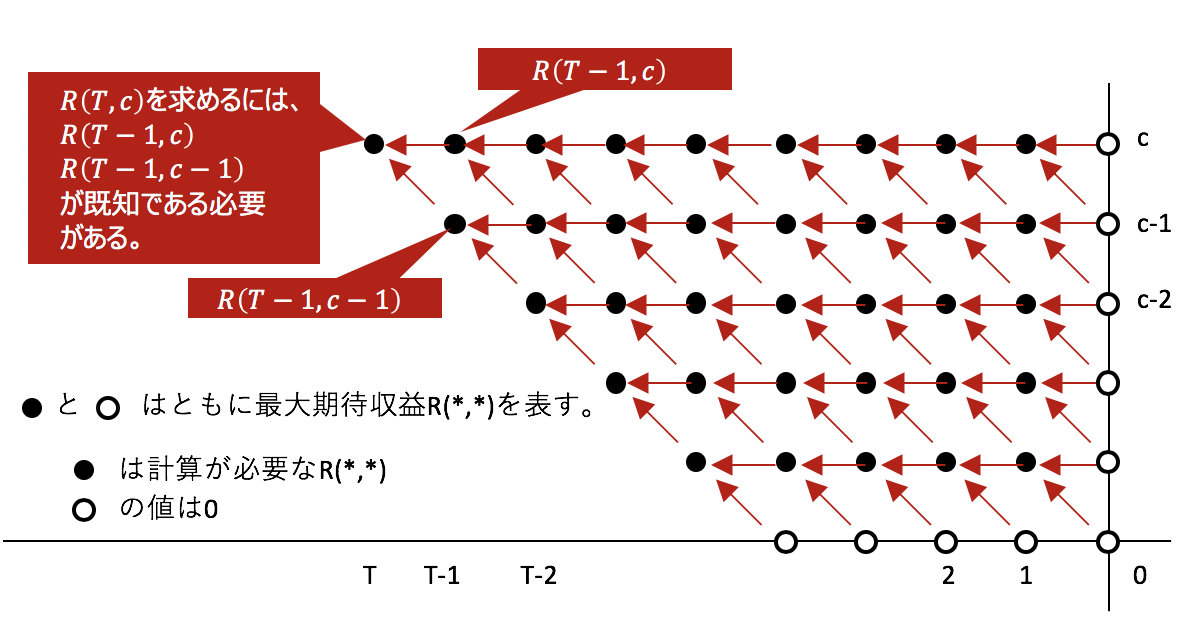
と書くとする。このとき、
と
が既知ならば、「最適性の原理」より
は次の式で求まる
これにより、各を逐次的に解くことで、
が得られます(下図参照)。

まとめ
今回は、ダイナミックプライシングの定式化について紹介しました。紹介したのは、非常にシンプルなモデルですが、問題に応じて拡張/修正することで多様な問題に対応することができます。
現実の問題では、や
が明らかではないので、予測を行う必要があります。予測は過去データを元に、統計モデリングやAIにより実現します。高い精度で
や
が予測できれば、最適価格の精度も高くなることが期待できます。
動的計画法の適用は計算負荷が多大になりがちですが、設定価格のとりうる値を連続量として扱うことができるので、厳密性の高い最適価格を求めることができます。とは言え、現実的には設定価格
のとりうる値は有限離散的であるケースがほとんどであると思われます。そのような場合は、整数計画問題として定式化し、線型緩和により最適値計算の高速化を図る、などのアプローチが考えられます。
現実の問題における、これらの具体的な対処法はノウハウや経験が問われるところです。当社はこれまで培ってきた多様なノウハウ・経験を生かし、ダイナミックプライシングの実現に取り組んでいます。
ダイナミックプライイングの活用法を分かりやすく解説したこちらのブログもご覧ください!
ai.brainpad.co.jp
ブレインパッドは、さまざまな取り組みを積極的に実施しています。実際のビジネスで自分の知識・技術を活用してみたいという方、ぜひエントリーください!www.brainpad.co.jp
*1:現状では、「ダイナミックプライシング」という言葉が指し示す内容は人によってまちまちなようです。また、レベニューマネジメントとダイナミックプライシングの区別は特に微妙で、人や文献によってかなり異なります。
*2:Marn, M. V., & Rosiello, R. L. (1992). Managing price, gaining profit. Harvard business review, 70(5), 84.(邦訳が「DIAMONDハーバード・ビジネス・レビュー 2001年04月号」に掲載されている)
*3:Sahay, A. (2007). How to Reap Higher Profits With Dynamic Pricing. MIT Sloan Management Review, 48(4), 53.
*4:厳密な議論については、例えば次の文献を参照してください:Gallego, G., & Van Ryzin, G. (1994). Optimal dynamic pricing of inventories with stochastic demand over finite horizons. Management science, 40(8), 999-1020.
*5:在庫補充ありの場合や、販売期間が有限でない場合のダイナミックプライシングの研究も存在しますが、ここでは述べません。
