トップ > まなぶ > Minimum Covariance Determinantを用いた異常検知

Minimum Covariance Determinantを用いた異常検知

まなぶ

本記事は、当社オウンドメディア「Doors」に移転しました。

約5秒後に自動的にリダイレクトします。

クレジットカードの不正利用検出などに代表される異常検知。今回のブログは、「Minimum Covariance Determinant」という共分散行列推定手法を用いた異常検知についてご紹介します！


こんにちは、アナリティクスサービス本部の安田です。

今回は、「Minimum Covariance Determinant」という共分散行列推定手法を用いた異常検知について、ご紹介します。

そもそも異常検知（Anomaly detection）というのは、データから「いつもとは異なる振舞い」（＝異常値）を見つけて、物体や事象の異常を見つけることです。

代表的な例としてよく見聞きするのは、クレジットカードの不正利用検出などですね。 これは、いつもと違うクレジットカードを用いた購買行動を観測することで、泥棒などによる不正利用を発見することです。不正利用を見つけることができれば、カード会社は口座を凍結するなどの対策を取ることができます。

こうやって我々のクレジットカードも守られているということを考えると、少し異常検知が身近に感じられますよね。

そして、タイトルにもある「Minimum Covariance Determinant」は、異常値や外れ値に対して頑健な分散共分散行列を推定するためのアルゴリズムです。

詳細はこれから紹介しますが、「Minimum Covariance Determinant」はあくまでも共分散行列を推定するための手法です。そのため異常検知だけではなく、主成分分析などの共分散行列に関係するさまざまな手法、アルゴリズムに対して応用可能です。

この分野は、今もなお関連する研究がなされており、個人的にもとても興味深いと感じたので本ブログで紹介させていただきます！

■目次

■異常検知の基本的な手法について

異常検知の手法としてはさまざまなものが知られていますが、その中でも最もナイーブな手法としてデータに多変量正規分布を仮定するものがあります。

多変量正規分布とは、次のような確率密度関数を持つ多次元の確率分布です。

$$ \begin{equation} f(\mathbb{x}; \mathbb{\mu}, \Sigma) = \frac{1}{\sqrt{(2\pi)^{d}|\Sigma|}}\exp\left[-\frac{1}{2}(x - \mu)^{T}\Sigma^{-1}(x - \mu)\right] \end{equation} $$

多変量正規分布はデータの生成過程に関する知見が無い場合に、最も自然と考えられる確率分布です。異常検知の枠組みでは、この分布を仮定したときに確率的に起こりにくい値を異常値とみなします。

ではどうやって確率的に起こりにくい値かどうかを判別するかのというと、マハラノビス距離を用います。

マハラノビス距離とは以下で定義される、共分散行列（つまり、分散と相関）を考慮した平均からの距離です。

$$ \begin{equation} MD(\mathbb{x}) = \sqrt{(\mathbb{x} - \mathbb{\mu})^T\Sigma^{-1}(\mathbb{x} - \mathbb{\mu})} \end{equation} $$

比べると一目瞭然ですが、多変量正規分布の密度関数の中にマハラノビス距離の二乗が含まれていることがわかります。これは、マハラノビス距離が大きいほど多変量正規分布の確率密度は小さくなる（⇔確率的に起こりにくい）ということを意味しています。

マハラノビス距離を用いて実際に異常度を測る場合は、データから標本平均と標本共分散行列を推定して、上記の式に代入することでそれぞれのデータの標本平均からの距離を計算します。

また、マハラノビス距離がどのくらい大きければ異常と判断するかは、マハラノビス距離が従う分布を利用する方法や、あらかじめ異常値だとわかっているデータがあれば、最もよく異常を捉えられるように閾値を設定する方法（=validation）などが用いられます。

しかしながら、マハラノビス距離の計算に必要となる標本共分散行列は学習データに異常値が混ざっているとそれに大きく引きずられてしまい、正常データだけを用いて推定を行った場合と大きく結果が異なってしまいます。

以下はそのイメージ図です。

青い点が正常データ、オレンジの点が異常データ、青い実線が正常データのみを用いて共分散行列を推定したときのマハラノビス距離の等高線、赤い点線は異常データも混ぜて推定したときのものです。

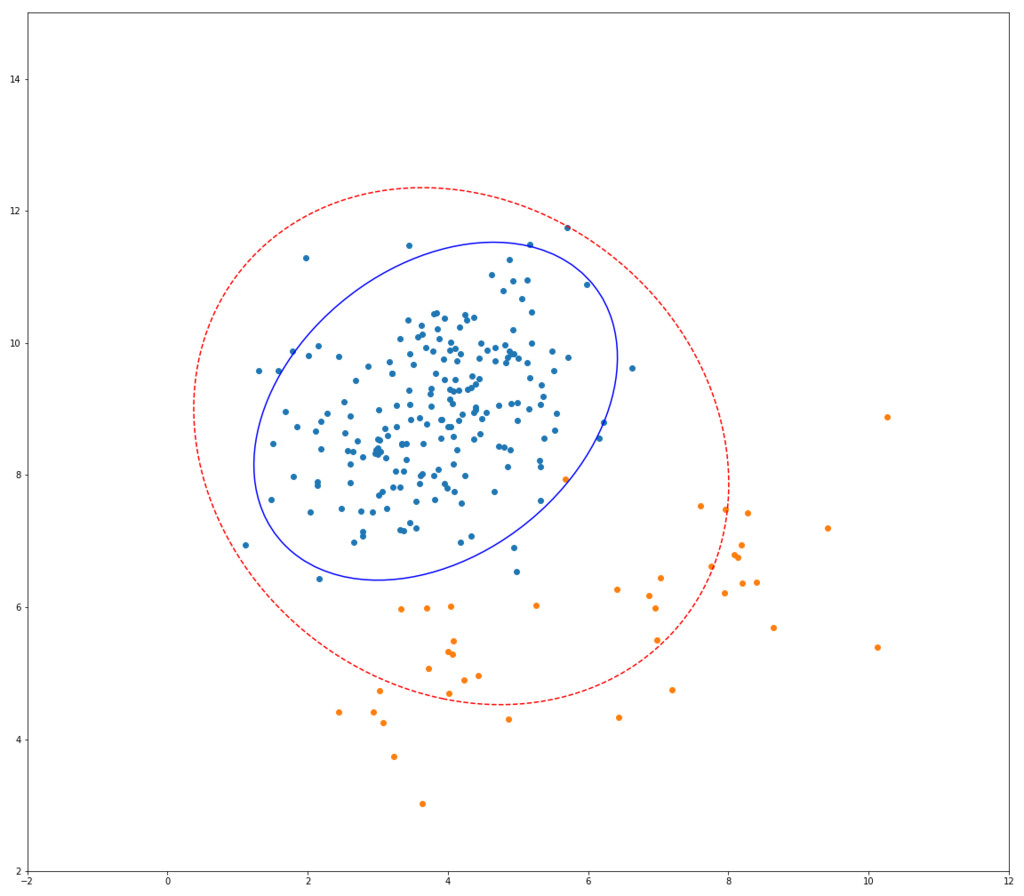
正常データのみで学習した場合と異常値を混ぜて推定した場合とで、大きく結果が違っていることが見て取れます。

学習データに異常値が混ざっていなければ問題無いのですが、実際の異常を検知するシチュエーションでは学習データに異常値が混ざっていてかつ、そのうちどれが異常なのかがわからない場合が往々にしてあります。そのような場合だと、上記の単純なマハラノビス距離を用いた異常検知手法が、機能しないであろうことは想像に難くありません。

そのため、異常値が混ざっているデータを用いて推定しても、正常データだけを使って推定した場合と大きく結果が異ならないような共分散行列推定手法が必要となります。

■Minimum Covariance Determinantについて

異常値に対して頑健って？

冒頭でも説明しましたが、Minimum Covariance Determinant（以下MCD）というのは、異常値に対して頑健な共分散行列の推定アルゴリズムです。

統計学において、頑健（robust）というのは、異常値（外れ値）に対してであったり、分布に対してであったりといくつかの意味で用いられます。そのため、本来であれば「～に対して頑健」と書くのが正確だと思うのですが、以下では異常値に対してという意味で単に頑健と表記します。

頑健とは何か？と聞かれたとき、はっきりとした定義はやや曖昧ですが、基本的には対象が何であれ、ある手法、モデル、推定量などが前提とする仮定を完全には満たさない状況でも、その結果が大きく変化しないことを指しているのだと考えています。（例えば、異常値に対して頑健であるというならば、異常値がデータに多少入っても推定量が大きく変わらないなど）

今回は簡単に実施できるように、異常値の定義に関しては、データの大部分とは明らかに異なる特徴を持つデータ程度にしておきます。異常値に対して頑健な推定量としては、中央値や刈り込み平均などが知られています。

頑健性を図る指標としては、以下の２つがよく知られています。

  • breakdown value
  • influence function

詳細に関してはここでは触れませんが、簡単な意味と例だけをご紹介します。参考程度なので以下は読み飛ばしていただいて構いません。

まず一つ目のbreakdown valueについてですが、簡単に説明すると標本の一部を任意の値に変更したときに, 推定値を \infty にするために必要な標本比率です。確率分布の位置を決定するlocation parameter（位置母数）の推定量（標本平均や中央値など）に対しては、

$$ \begin{equation} \epsilon^{* }_{n}(T_n; X_n) = \frac{1}{n}\min\{m \in 1,\ldots, n\} :\sup_m||T_n(X_n)-T_n(X_{n, m})||=+\infty\} \end{equation} $$

のように定義されます。（ここで X_nはサンプルサイズ nのデータ、 X_{n, m}はX_nの内m個を任意の値に変えたもの、T_n(\cdot) はlocation parameterの推定量）

標本平均の場合、このbreakdown valueは 1/nとなり、無限標本系 (n\to\infty) では0となります。

イメージとしては、次のような感じです。

データ点を20個用意しました（青い点）、そしてこれらの標本平均を赤い点、中央値を黄色い点で表しています。

このサンプルの1つをどんどん \infty に近づけていった様子を、以下のアニメーションに書いています。

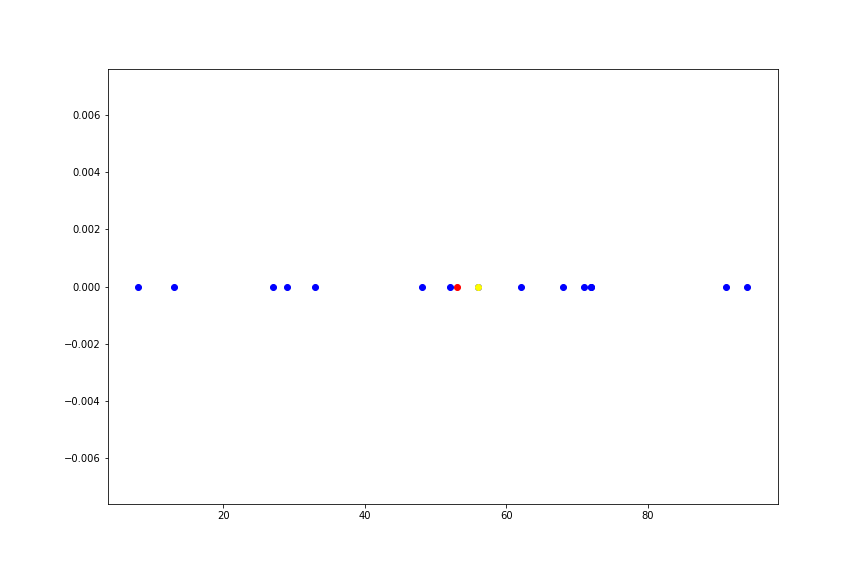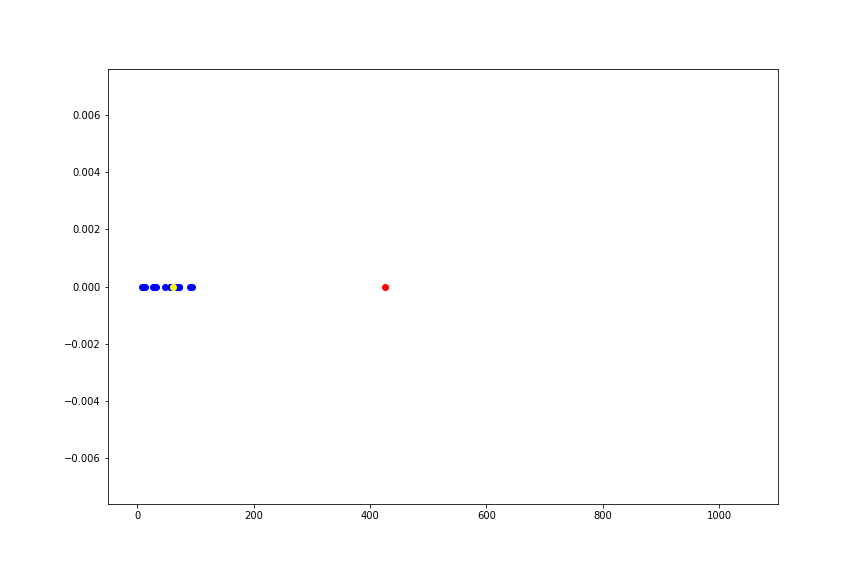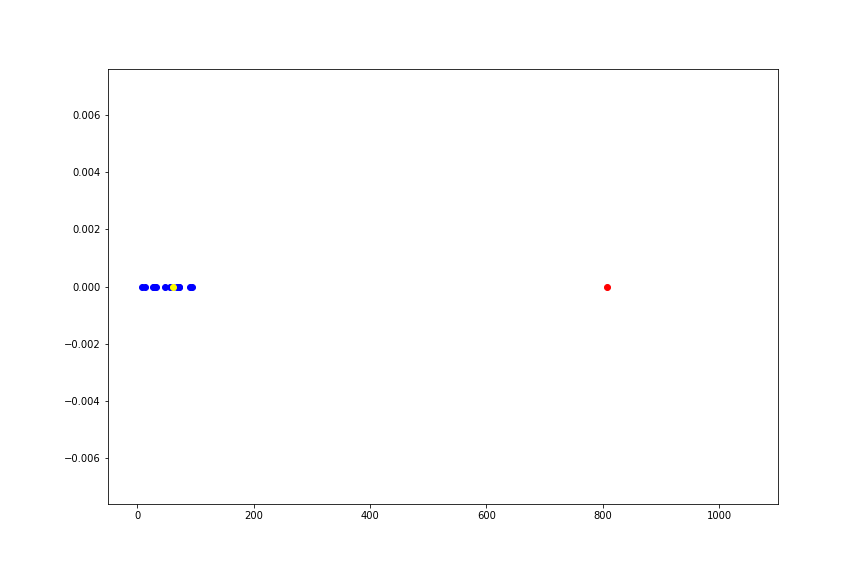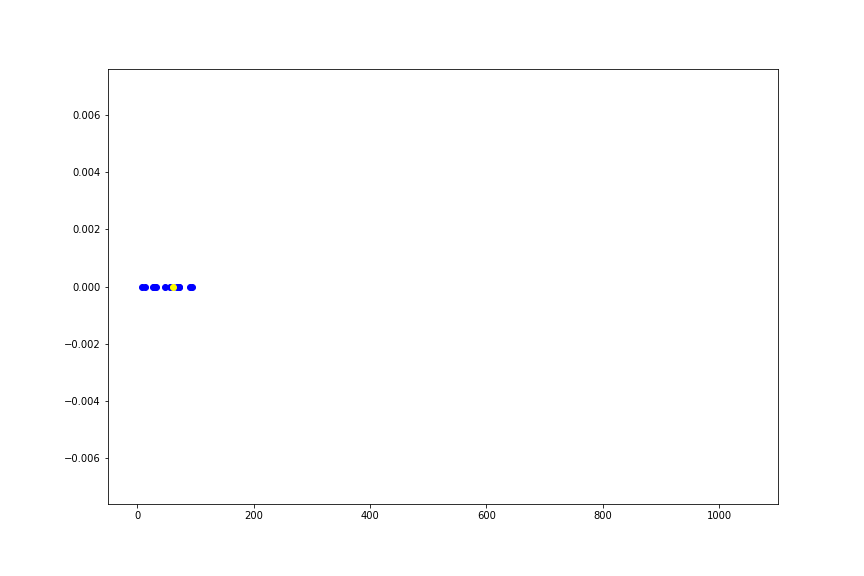
このようにデータのうち、たったひとつの値を極限に持っていくだけで標本平均という推定量は、データの分布の位置を示すという本来の意味をなさなくなってしまいます。 一方、中央値は全く変動しません。

実際は、 \infty のような極端な値を取ることはまずないと思いますが、桁が1つや2つ違う異常値が紛れることは、まぁまぁあります。

ちなみに、中央値のbreakdown valueは無限標本系において0.5となります。これはつまり、データの半分の値を極限に持っていかなければ \inftyにならないことを意味しており、中央値が非常に頑健であることがわかります。

上記のbreakdown-valueが、推定量を崩壊させるためのデータの変更数に注目していたのに対して、もう一つのinfluence functionはデータを変更させたときの推定量の変化を確認するものです。

$$ \begin{equation} IF(\mathbb{x}, T, F) = \lim_{\epsilon \to 0}\frac{T(F_{\epsilon}) - T(F)}{\epsilon} \end{equation} $$

ここで、Fは任意の確率分布、 Tは Fのパラメータの推定量, F_{\epsilon} = (1-\epsilon)F + \epsilon\Delta_{x}はFに微小な変化を与えたものです。

Influence functionが大きい場合、データが変わると推定量も大きく変わる可能性があり、頑健性が低いとみなされます。

このような指標を用いて、推定量の頑健性が確認されます。

Minimum Covariance Determinant（MCD）って？

さて、前置きが長くなりましたが、本題のMCDの説明に入ります。

MCDとは頑健な共分散行列を推定するためのアルゴリズムです。どのように頑健な共分散行列を推定するかというと、データの中から予め決めた割合の標本を抽出して共分散行列を推定する操作を繰り返し、その行列式が最小となるようなデータの組合せから推定した共分散行列の推定値を求めます。

共分散行列の行列式最小？と思われると思いますが、この（個人的な）直感的理解を以下に述べます。

まず任意の行列に対して、行列式は以下のようにその固有値の総乗で表せます。

$$ \begin{equation} |\Sigma| = \prod_{j} \lambda_j \end{equation} $$

ここで \lambda_j は、行列 \Sigma の固有値です。

特に共分散行列の場合、固有値は主成分分析の主成分の分散に一致します。 つまり共分散行列の行列式最小とは、主成分の分散の積（＝データのちらばり）が一番小さくなることを意味しています。

より密集している部分のデータのみを使えば異常値が混ざらなさそう、というのは感覚と一致するのではないでしょうか。

また、MCD推定量には「Affine equivalent」と呼ばれる、以下のような良い性質があります。

$$ \begin{align*} \hat{\mu}_{MCD}(AX + \mathbb{b}) &= A\hat{\mu}_{MCD}(X) + \mathbb{b}\\ \hat{\Sigma}_{MCD}(AX + \mathbb{b}) &=A\hat{\Sigma}_{MCD}(X)A^{T} \end{align*} $$

ここでAは非特異の行列、\mathbb{b}は定数のベクトルです。

つまり、推定を行った後、データの場所を一律に動かそうが、回転を加えようが同じ処理をその推定値に行えば、変更後のデータに対して推定を行った結果と同じになるということです。

これが何の役に立つのか？と思われるかもしれませんが、データ解析の場面でよく行われる、標準化や無相関化（白色化）がAffine equivalentな変換にあたるので、これらの操作の際にも再計算をしなくて良いことが担保されているのは、大きいです。もちろん、標本平均や標本共分散行列にもこの性質はあります。

これで、MCDの大まかな仕組みがわかりました。なので、標本の一部を取ってきて、共分散行列とその行列式を計算。これをすべての組合せに対して行って、行列式が最小になるようなものが最良！！！.... とできれば良いのですが、実際は計算時間の都合から困難です。

そのため、実応用に耐えうる高速な次のアルゴリズムが考案されています。

Fast-MCDについて

先程述べたように、もともとのMCDは非常に計算量が多いです。仮にサンプルサイズが1万で、そのうちの0.1%を取り除くとすると _{10000}C_{10}\simeq 2.74\times10^{33} という途方もない組合せ数の計算量を必要とします。

これは、すべての組合せを計算しているために時間がかかるのですが、我々の目的は共分散の行列式が最も小さくなるサンプルの組合せを見つけることです。そのため、何らかの基準で、常に「今まで計算したものよりもより小さい行列式をもつサンプルの組合せ」を見つけることを繰り返せばよい、というのがこれから説明するFast-MCDの考え方です。

具体的には、次の手順で計算を行います。

\mathbb{x}_i を p 次元確率ベクトルとしたとき、X = \{\mathbb{x}_1, \dots, \mathbb{x}_n\} とする。
また、H_{old}\subset X を X からランダムに抽出した大きさ h の \mathbb{x}_i の集合とする。

1. H_{old} の平均ベクトルと共分散行列をそれぞれ \hat{\mathbb{\mu}}_{old}, \hat{\Sigma}_{old} とする。
2. \hat{\Sigma}_{old} の固有値 |\hat{\Sigma}_{old}| を計算する。
3. \hat{\mu}_{old}, \hat{\Sigma}_{old} を使ったマハラノビス距離を X の各要素に対して計算し、
d(\mathbb{x}_i):= \sqrt{(\mathbb{x}_i - \hat{\mu}_{old})^T\hat{\Sigma}^{-1}_{old}(\mathbb{x}_i - \hat{\mu}_{old})} とする。
4. d(\mathbb{x}_i) を小さいもの順に並べ、d_{j:n} をその中で j 番目に大きいものとする
（d_{1:n} \leq \dots \leq d_{j-1:n} \leq d_{j:n} \leq d_{j+1:n} \leq \dots \leq d_{n:n}）。
5. H_{new} := \{d_{1:n}, d_{2:n}, \dots, d_{h:n}\} とする（つまり, d_{j:n} を小さいもの順に h 個取ってくる）。
6. H_{new} の平均ベクトル、共分散行列とその固有値 \hat{\mathbb{\mu}}_{new}, \hat{\Sigma}_{new}, |\hat{\Sigma}_{new}| を計算する。

上記を |\hat{\Sigma}_{new}| = 0 となるか、|\hat{\Sigma}_{old}| - |\hat{\Sigma}_{new}| が十分小さくなるまで繰り返す。

こうして、最終的に得られた平均ベクトルと共分散行列が異常値に対して頑健なMCD推定量となります。

また上記アルゴリズム中で、|\hat{\Sigma}_{new}| \leq |\hat{\Sigma}_{old}| （等号条件は \hat{\mu}_{old} = \hat{\mu}_{new} かつ \hat{\Sigma}_{old} = \hat{\Sigma}_{new}）となることが知られています。

計算した共分散行列を用いたマハラノビス距離を使ってデータの並び替えを行えば、「より平均から遠いデータを取り除くことができる」というのは自然な考え方ですね。

上記Fast-MCDのアルゴリズムが実際にどう動いているのか、以下にシミュレーションイメージを示します。 それぞれ、青い点が正常データ、オレンジの点が異常データ、赤い点線の楕円が一般的な方法（最尤法）で推定した共分散行列を用いたマハラノビス距離の等高線、青い線の楕円がMCDによるものです。

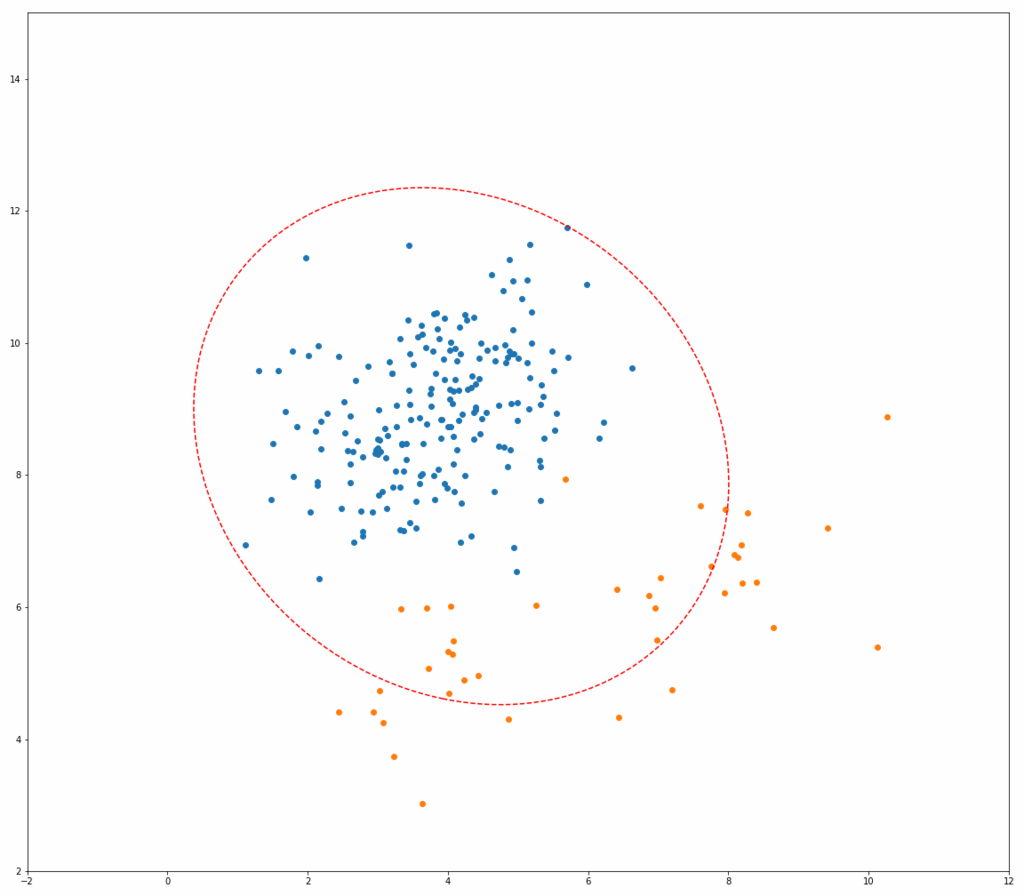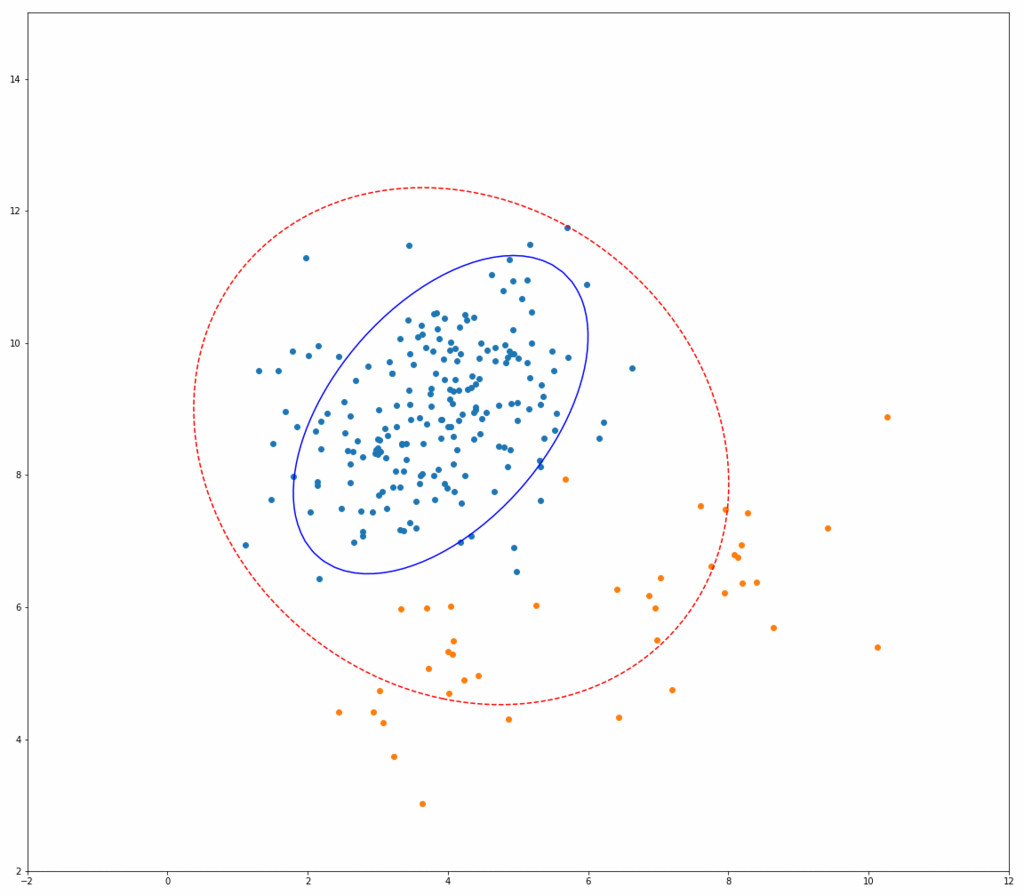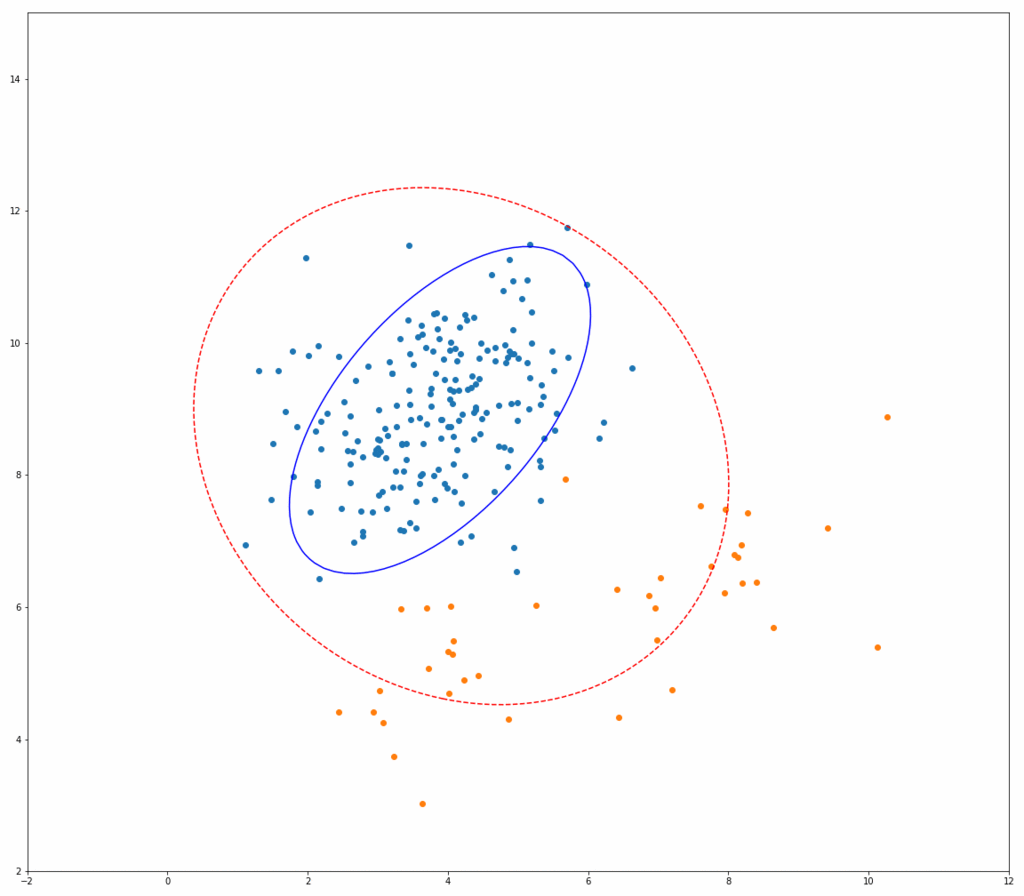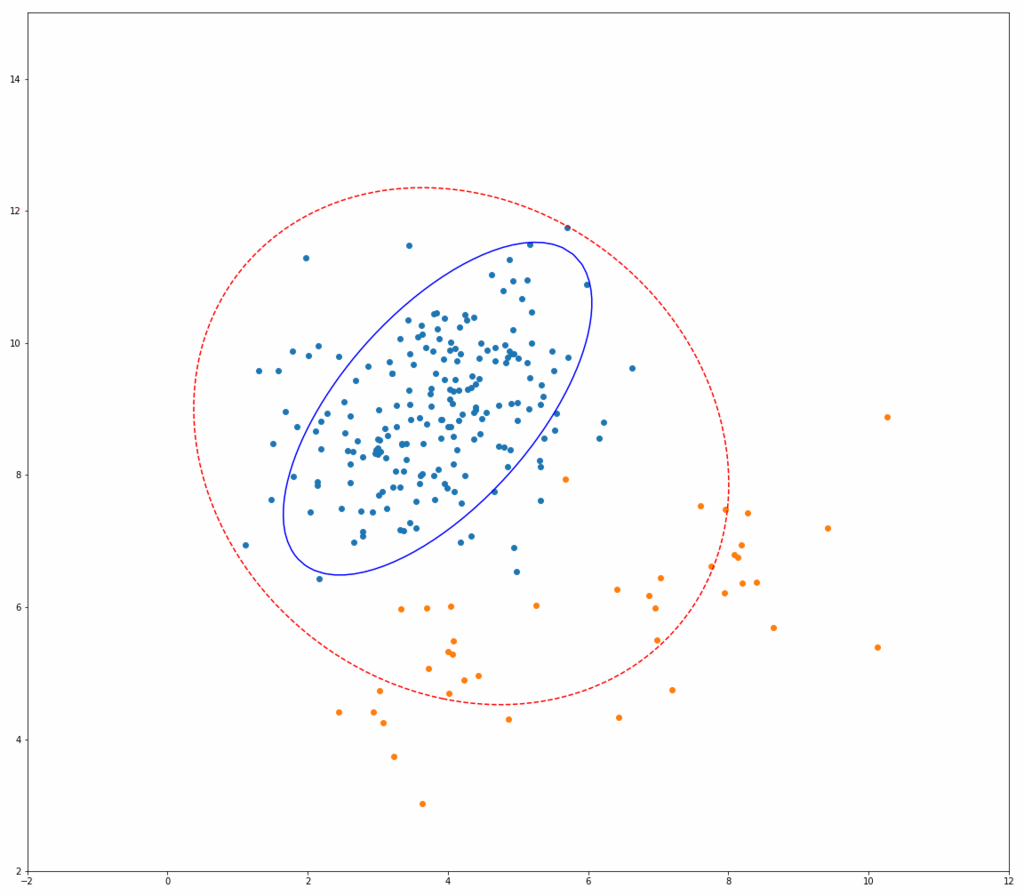
繰り返しを行うごとに、青い楕円がどんどん正常データだけを囲んでいく様子がわかると思います。

■sklearn.covariance.MinCovDetを使って異常検知してみる

それでは、実際にMCDをつかってデータの異常を捉えられるか、やってみたいと思います。 pythonのscikit-learnの中には、Fast-MCDを実装したsklearn.covariance.MinCovDetがあるので、今回はこれを使います。

データには信頼と実績のフィッシャーのirisデータに乱数で発生させた異常を乗せ、これを検知できるかを試します。 irisデータには、それぞれサンプルサイズ50ずつで 'setosa', 'virginica', 'versicolor' という三種類のあやめのデータがありますが、この内、'virginica'と'versicolor'を正常データとして用います。 また、異常データは正常データから少しずらした位置に適当に20個発生させます。

import numpy as np
import pandas as pd
from sklearn import datasets
from scipy import stats

# 正常データの設定
iris = datasets.load_iris()

df_normal = pd.DataFrame(iris.data[iris.target>=1], columns=iris.feature_names)

# 異常データの設定
anomaly_params = dict(
    mean=df_normal.mean() + [1, -0.5, -1, 0.5],
    cov=np.array([[0.3, 0.1,0.1,0.1], [0.1, 0.3,0.1,0.1], [0.1, 0.1,0.3,0.1], [0.1, 0.1,0.1,0.3]]),
    size=20,
    random_state=3655
)
df_anomaly = pd.DataFrame(stats.multivariate_normal.rvs(**anomaly_params), columns=iris.feature_names)

df_normal['label'] = 'normal'
df_anomaly['label'] = 'anomaly'
df_data = pd.concat([df_normal, df_anomaly])

上で作ったデータの対散布図です。 青い点がirisを使った正常データ（'virginica'と'versicolor'）、オレンジが乱数を用いて発生させた異常データです。

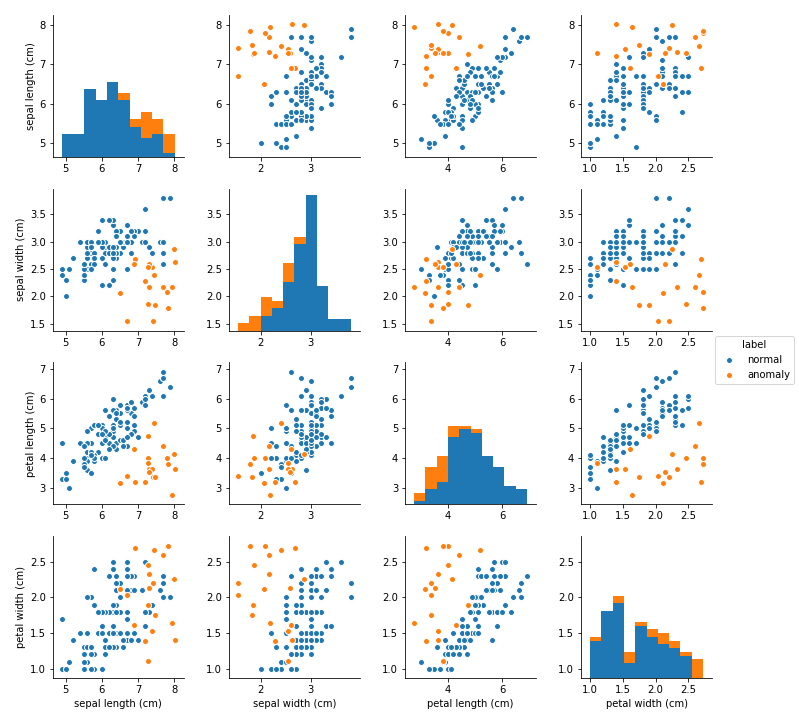
この内の3割をテストデータとして取っておいて、残りの学習データに対して、それぞれ最尤法とMCDを使って推定したマハラノビス距離を用いて、異常を検知できるか比較します。

from sklearn.model_selection import train_test_split

# データを7:3で学習用とテスト用に分割
df_data_train, df_data_test = train_test_split(df_data, test_size=0.3, random_state=3655)

df_x_train = df_data_train.drop('label', axis=1)
df_x_test = df_data_test.drop('label', axis=1)

学習は、sklearnで共通のfitを使います。 また、マハラノビス距離の二乗の算出は、mahalanobisで可能です。

from sklearn.covariance import EmpiricalCovariance, MinCovDet

# MCD
mcd = MinCovDet()
mcd.fit(df_x_train)
anomaly_score_mcd = mcd.mahalanobis(df_x_test)

# 最尤法
mle = EmpiricalCovariance()
mle.fit(df_x_train)
anomaly_score_mle = mle.mahalanobis(df_x_test)

以下の結果を示します。 上の図がMCD、下の図が最尤法を用いたときの各テストデータに対する異常度のプロットです。横軸は各データのindex、縦軸はマハラノビス距離（⇔異常度）を表しています。

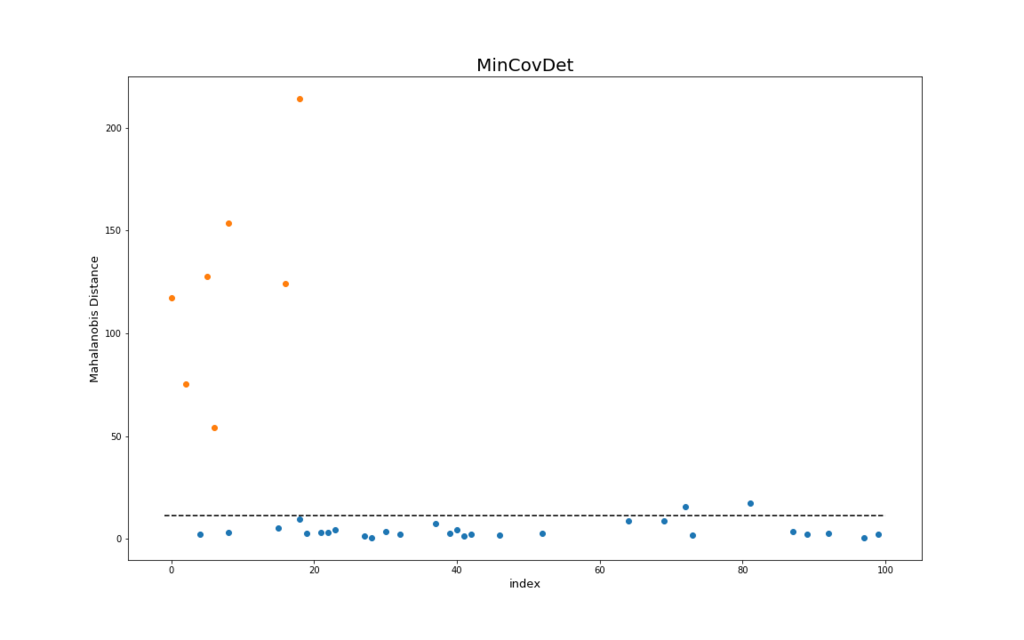
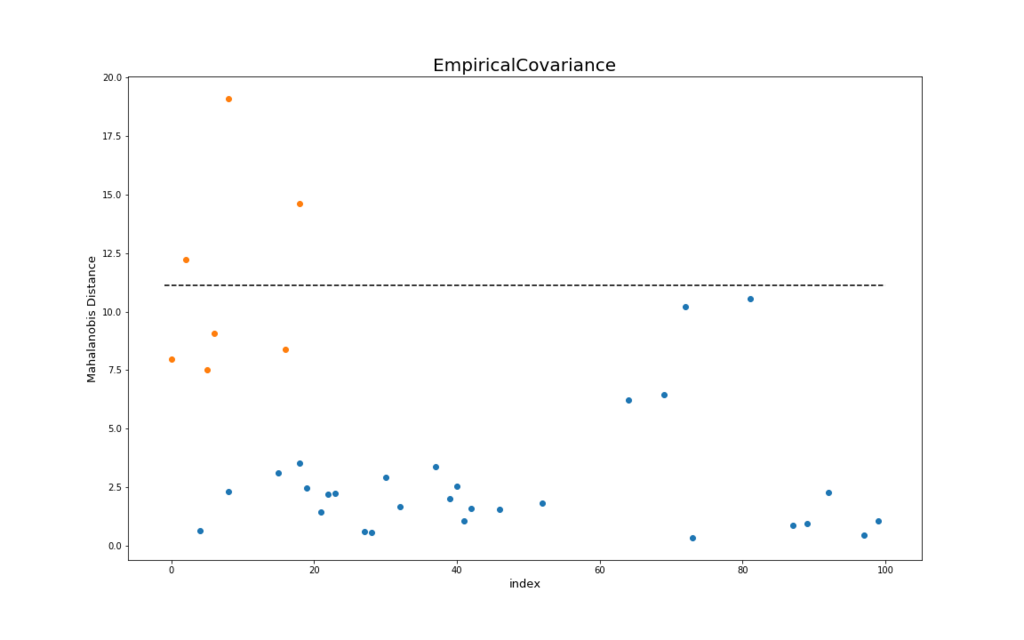
これも同様に、青い点が正常データ、オレンジの点が異常データを示しています。 また、黒い点線は自由度が4のカイ二乗分布の左側97.5%点 （ \chi^{2}_{4, 0.975}）を目安として示しています1。

MCDは閾値を点線よりも少し大きく取れば、正常データと異常データが完全に分離できるのに対して、最尤法の方は2つの正常データを幾つかの異常データよりも異常度を高く算出しています。

またMCDは、縦軸のスケールが最尤法よりも大きくなっています。これも異常データに対して、より強くその異常度を示していることを表しています。

■まとめ

今回はナイーブな手法に少しアレンジを加えた異常検知について、紹介させて頂きました。最近は、深層学習を用いた異常検知が精度もよいので流行っており、弊社でも取り組んでいます。

しかし、たまにはこのようなアルゴリズムに触れるのも良いのではないでしょうか。

■参考文献

  • Minimum Covariance Determinant
  • sklearn.covariance.MinCovDet
  • A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS
  • Asymptotics For The Minimum Covariance Determinant Estimator, The Annals of Statistics, 1993, Vol. 21, No. 3, 1385-1400
ブレインパッドは、さまざまな取り組みを積極的に実施しています。実際のビジネスで自分の知識・技術を活用してみたいという方、ぜひエントリーください！

www.brainpad.co.jp

  1. 推定量を差し込んだ場合のマハラノビス距離は、その推定量に対応してカイ二乗分布とは異なる分布に従うことが知られています。↩