本記事は、当社オウンドメディア「Doors」に移転しました。
約5秒後に自動的にリダイレクトします。

Table of Contents
- イントロダクション
- 予算配分最適化
- 包絡分析法(Data Envelopment Analysis, DEA)
- Free Disposal Hull (FDH)
- 予算配分最適化への適用例
- まとめ
- 参考文献
イントロダクション
こんにちは、アナリティクスサービス本部の加藤です。現在私は研究開発グループの下で新たなデータ分析手法の研究開発の仕事に携わっています。
研究開発グループでは、ブレインパッドに依頼されるデータ分析案件の品質向上を目的に、新たな分析手法の調査・開発と、実用化を目指しています。様々な研究テーマがある中で、私は予算配分最適化というテーマを扱っています。
今回のブログでは、私達が予算配分最適化に利用している包絡分析法を中心に、分析手法の紹介をしたいと思います。
最後に適用例として、これらの分析法をどのように予算配分最適化に活かすかを紹介させていただきます。
予算配分最適化
予算配分最適化では、各メディアにどのように予算を配分すれば利益が最大化するか、という問題について検討します。
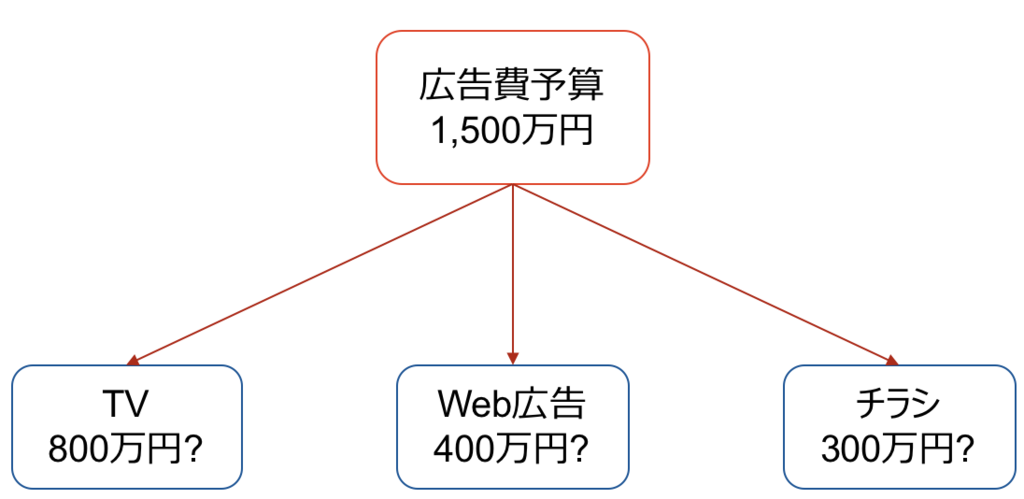
例えば、広告費の予算として1500万円があったとき、それをどの出稿媒体に、どのように配分するかを決定する、といった問題です。
予算配分最適化では、まず過去の出稿実績からシミュレータの作成を行い、そのシミュレータをもとに利益を最大化する予算配分を求めます。
シミュレータの作成に今まで使われてきた手法としては、
- 重回帰分析
- 構造方程式モデリング(SEM)
- 状態空間モデル
- 機械学習
などが挙げられます。
それぞれ分析手法としては有用なのですが、予算配分最適化への応用は様々な仮定を置く必要があります。
例えば重回帰分析を図1の例に適用する場合、を売上、
をそれぞれの出稿媒体費、
を対応するパラメータと考えて、
という式で表されます。
しかし、テレビCMとWeb広告の間に相乗効果がある場合、この式では相乗効果を表すことができません。そのため、各媒体の相乗効果を考慮した項をモデルに加える必要がありますが、どのメディア間に相乗効果が存在するのか主観的な仮説はあっても客観的には分かりません。
このような場合、考え得る全ての相乗効果を式に追加することもできますが、モデルのパラメータが多くなってしまい、パラメータの推定には多くのデータが必要になります。
広告への出稿実績とその売上に関するデータは一般的に観測数が少ないため、パラメータが多いモデルの学習は難しいです。
現実的に得られるデータとしては、日単位または週単位の
- 各出稿媒体の実績
- 総売上
だと考えられるため、これらのデータを利用して予算配分最適化が行える分析手法が必要とされます。このような手法の1つが包絡分析法となります。
包絡分析法(Data Envelopment Analysis, DEA)
包絡分析法(Data Envelopment Analysis, DEA)は、入力に対する出力の効率性の評価をする手法の一つです。効率性を評価する指標としてまず思いつくのは、入力に対する出力の比率だと思います。
例えば、複数店舗を持つ商店のコストを入力、売上を出力とし、
各店舗の効率性を評価する場合を考えます。この場合は(売上/コスト)の値で比較を行うと、効率よく利益をあげられた店舗が定量的に評価できます。
では、更に詳細に効率性を評価する場合を考えます。各店舗の広さや店員の数も入力として考慮する場合、単純な比率(出力/入力)では評価ができません。
このような多入力・多出力の場合に効率性の評価をする時、包絡分析法が有用です。
以下では包絡分析法と、包絡分析と似た分析手法であるFree Disposal Hull・Interpolated Free Disposal Hullについて簡単に紹介します。
包絡分析法の考え方
簡単にするためにコスト総額と売上総額について考えてみます。
このように、1つの入力(コスト)に対して1つの出力(売上)の関係を考える場合は、入力値と出力値を2次元平面にプロットできるため、可視化が簡単です。

包絡分析法では分析対象(つまりプロットの一つ一つ)をDMU(decision making unit, 意志決定者)と呼びます。 ここで挙げている例ではDMUはある日の(コスト,売上)の組で記述されます。
包絡分析法として解くべき問題を簡単に言うと、図2でプロットされている点を全て覆うことのできる線(包絡線)を求めよ、というものになります。
この包絡線のことを効率的フロンティアと呼び、効率的フロンティアに囲まれた内側の領域を生産可能集合と呼びます。
効率的フロンティアは、「これまでの実績に基づいて考えると、最も効率が良い実績はこの線上に乗るはずだ」ということを意味しています。
また、生産可能集合に含まれているDMUは「効率的なDMUと同じコストをかけて売上が少ないDMU」、もしくは「効率的なDMUと同じ売上を出すために多くのコストがかかったDMU」と考えることができます。
例として挙げたものが2次元で図示できるため、効率的フロンティアを求めることは一見簡単に思えますが、多入力・他出力の場合は難しいです。
例えば、コストとして商品の仕入れにかかったコスト、広告にかかったコストの2点に着目する必要があれば、これは入力が2つの問題になります。また、売上だけでなく、ホームページの来訪者数についても考えたい、となれば出力が2つの問題になります。
そのため、一般には高次元の空間中にプロットされたデータ点を囲う包絡面を考える必要があり、目で見て決めるといったことは不可能になります。
実際には2次元で図示できるときも包絡線を目で見て決めているわけではなく、線形計画問題と呼ばれる数学の問題に落とし込んで考えます。
解くべき問題を数学の言葉で記述しておけば、何次元でも包絡線を求めることが可能です。
問題の設定の仕方によって、描かれる包絡線に違いが生じます。
以下で3つの例を紹介します。
CCR モデル
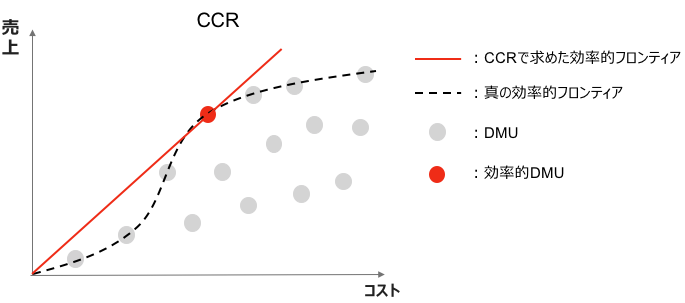
CCR(Charnes-Cooper-Rhodes)モデルは出力/入力の比が最大になるDMUを効率的なDMUと考えるモデルです。
1-入力、1-出力の例では、原点とDMUを結んだ直線が傾き最大となるように効率的フロンティアが決められます。
CCRモデルの評価基準はわかりやすいですが、このモデルでは効率的DMUが定まると入力値のスケールに関わらず効率的DMUの出力/入力の比が実現可能と考えるため、「1分で50回腕立て伏せができるデータがあるので、100分では5000回腕立て伏せできる」といった、考えている対象によってはあまり現実的ではない結果が得られることもあります。
BCC モデル

BCC(Banker-Charnes-Cooper)モデルは観測されているDMU全てを包み込む凸包を構成するモデルです。
CCRでは効率的DMUが1つでしたが、BCCでは凸包を構成しているDMUが全て効率的DMUになります。BCCモデルはCCRモデルと異なり、入力値のスケールによる効率性の変動が評価可能になります。
DRS モデル
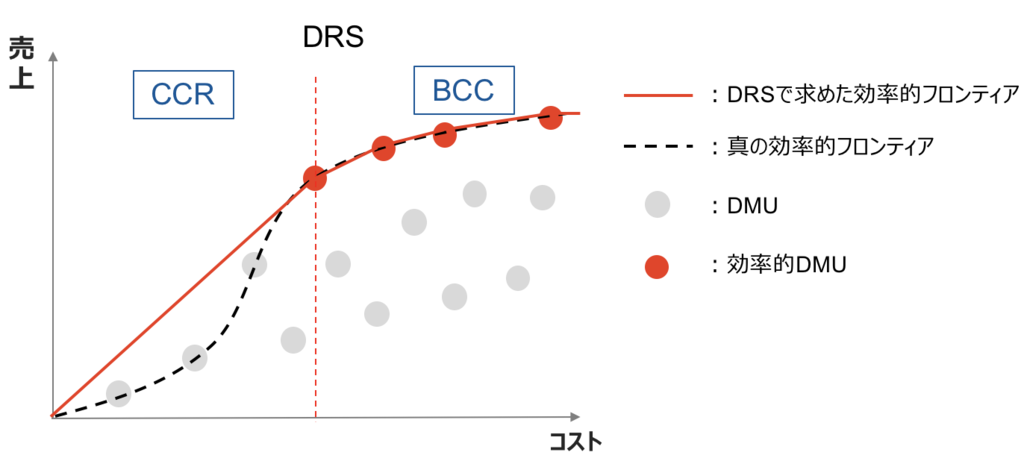
DRS(Decreasing Returns to Scale)モデルは原点もDMUと考えたBCCモデルです。
DRSモデルの特徴として、入力値が小さい領域ではCCRモデル、大きい領域ではBCCモデルの性質を持つ効率的フロンティアが構成されます。
包絡分析法の問題点
これまで挙げてきた包絡分析法の問題点は、"凹んでいる"場所にあるDMUを効率的DMUと認識できず、DMUの効率性を過小評価してしまうことです。
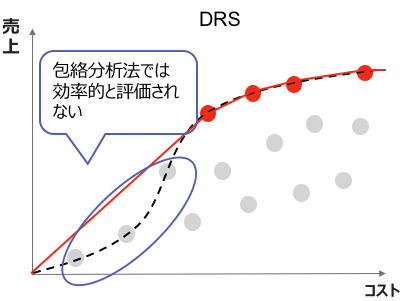
この問題に対応できる手法としてFree Disposal Hull(FDH)があります。
Free Disposal Hull (FDH)
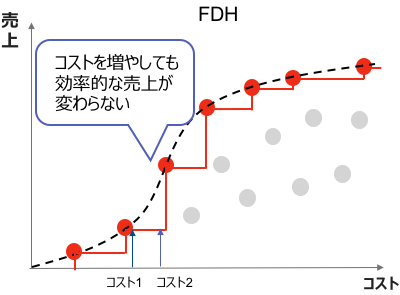
FDH

包絡分析法と同様にFDHでも効率的なDMUを考えるのですが、
フロンティアは効率的なDMUを階段状に繋いで構成されます(図7)。
FDHの効率的フロンティアは凹んでいる領域にあるDMUも適切な評価が可能ですが、冒頭で紹介したような予算配分最適化に利用することを考えると問題が生じます。
階段状のフロンティアは、入力の変化に対して出力が変わらない領域が存在しますが、そのような性質は予算配分最適化に悪影響を与えます(図8)。
iFDH
FDHのこの問題への対応策として、当社の研究開発グループと中央大学理工学部教授の生田目先生はInterpolated Free Disposal Hull(iFDH)を考案しました。
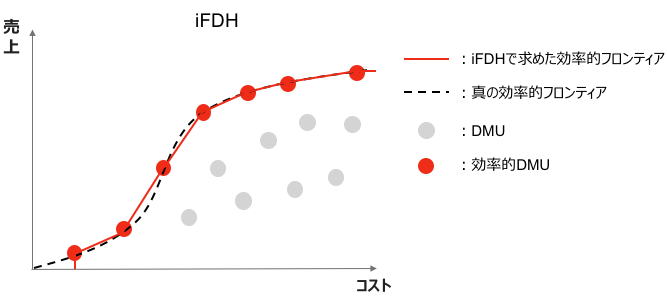
iFDHはまずFDHを行った後、効率的なDMUを直線で補間して効率的フロンティアを再構成します。
これまで挙げた例と同様に、図9では2次元(1-入力・1-出力)でプロットしているため補間は簡単ですが、多次元での補間は複雑になります。
iFDHについては昨年の6月に香港で行われた国際会議「ICIBM 2018」で当社の社員が発表させていただきました(香港で開催された国際会議「ICIBM 2018」発表レポート~広告予算配分の最適化~)。
iFDHによって、
- 凹んだ領域に対応
- 出力が一定にならない
という効率的フロンティアを構成することができるようになりましたが、予算配分最適化にどのように適用されるかを最後に紹介したいと思います。
予算配分最適化への適用例
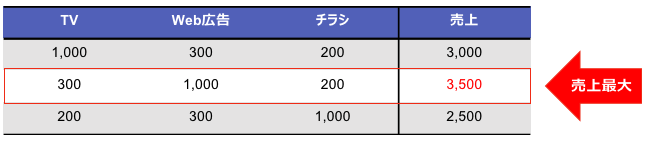
冒頭で挙げた広告費の例(図1)を考えてみます。
広告費予算として1500万円があったとき、それをどの出稿媒体に、どの配分で使うのが良いでしょうか?
この問題に対してiFDHを適用します。
過去の出稿実績を用い、日毎のメディア媒体費と売り上げをDMUとして、効率的フロンティアを求めます。そのフロンティアをシミュレータとして使えば、図10のように最適な予算配分が行えます。
まとめ
今回のブログでは、予算配分最適化をテーマに
予算配分最適化の考え方
既存手法の問題点と、包絡分析法を採用する理由
包絡分析法の考え方とモデル例
包絡分析法の問題点と、その対応としてのFDH・iFDH
予算配分最適化への適用
を説明しました。
今回は包絡分析法やFDH・iFDHについて、予算配分最適化への応用を目的として説明しましたが、これらの分析法は、入力に対する出力の効率性を評価する、という形の問題に広く適用が可能です。
ここでは説明できませんでしたが、多入力・多出力の効率性を評価してみると、それぞれのDMUがどんな特徴を持っているのか、改善のためにはどのようなことをしたら良いのか、といったことが定量的に評価でき、とても興味深いと感じています。
ブレインパッドでは、流行りの機械学習・深層学習を使った分析だけでなく、蓄積されたデータを定量的に評価し業務の改善に役立てることを目的に様々な手法で分析を行っております。
分析手法の簡単な紹介ではありましたが、興味を持っていただければ嬉しく思います。
参考文献
- 「経営効率性の測定と改善 -包絡分析法DEAによる-」刀根薫著, 日科技連出版社
- 「経営システム工学ライブラリー8 オペレーションズ・リサーチ」 森雅夫・松井知己著, 朝倉書店
- N. Tachibana, S. Kadoya, T. Noguchi, T. Namatame, "A Resource Allocation Method using a Non-parametric Approach," submitted
ブレインパッドは、さまざまな取り組みを積極的に実施しています。実際のビジネスで自分の知識・技術を活用してみたいという方、ぜひエントリーください!
